人工智能赋能的查询处理与优化新技术研究综述
1
2020
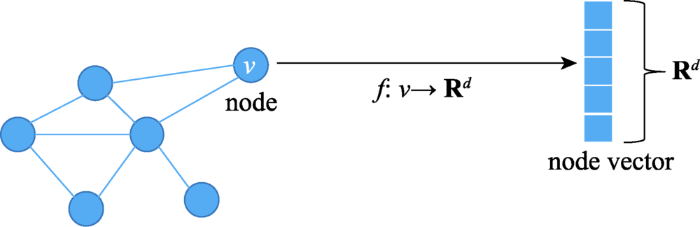
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
Survey on AI powered new techniques for query processing and optimization
1
2020
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
A novel approach to detect associations in criminal networks
1
2020
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
Attention based spatial-temporal graph convolutional networks for traffic flow forecasting
1
2019
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
Recent advances in convolutional neural networks
1
2018
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
Recent advances in recurrent neural networks
1
2017
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
Deep learning
1
2015
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
Node classification in social networks
1
2011
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
The link-prediction problem for social networks
1
2007
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
A min-max cut algorithm for graph partitioning and data clustering
1
2001
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
Visualizing data using t-SNE
2
2008
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
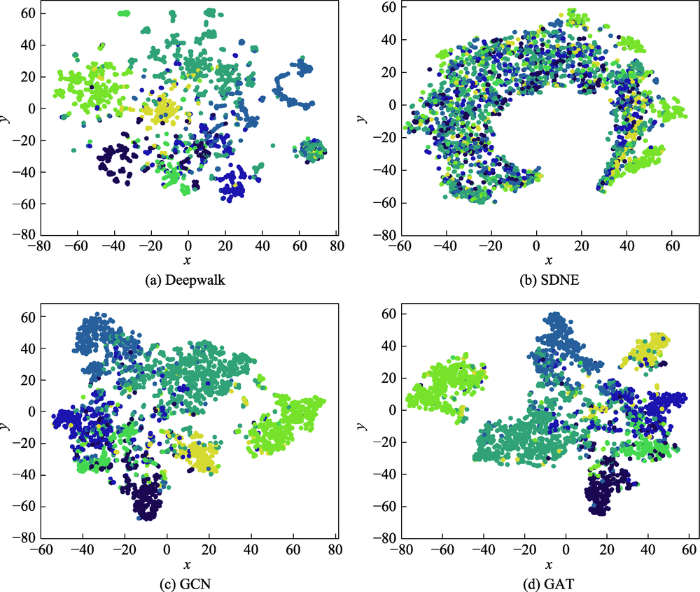
... 对于可视化任务,好的嵌入表示在二维图像中相同或相近的节点彼此接近,不同的节点彼此分离.在Cora数据集上,将模型生成的低维嵌入输入到t -SNE[10 ,152 ] ,使嵌入维数降至2,同一类别的节点使用相同的颜色表示.Yuan等人[153 ] 比较了不同模型的可视化性能,部分可视化结果见图28 .GCN和GAT学习的节点向量能够有效捕捉到社区的结构,使同类型节点更为接近.Deepwalk和SDNE只使用邻接矩阵作为输入,没有充分利用节点特征和标签信息,导致模型性能较差,尤其是SDNE模型,不同类型的点在二维空间中几乎是无序的. ...
DeepInf: social influence prediction with deep learning
1
2018
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
How good your recommender system is? A survey on evaluations in recom-mendation
1
2019
... 图是复杂系统中常用的信息载体,可以表示现实中许多复杂关系,如社交网络[1 ] 、犯罪网络[2 ] 、交通网络[3 ] 等.图结构作为一种非欧几里德数据,很难直接应用卷积神经网络(convolutional neural network,CNN)[4 ] 和循环神经网络(recurrent neural network,RNN)[5 ] 等深度学习方法[6 ] .为了构造用于图数据挖掘的特征表示,图嵌入将节点映射到低维空间,生成保留原始图中某些重要信息的低维向量.目前,图嵌入不仅在节点分类[7 ] 、链接预测[8 ] 、节点聚类[9 ] 、可视化[10 ] 等复杂网络上的机器学习任务中获得成功,还广泛用于社交影响力建模[11 ] 、内容推荐[12 ] 等现实任务. ...
Distributed large-scale natural graph factorization
3
2013
... 早期的图嵌入算法主要用于数据降维,通过邻域关系构建相似度图,将节点嵌入低维向量空间,并保持相连节点向量的相似性.这类方法通常时间复杂度高,很难扩展到大型图上.近年来,图嵌入算法转向扩展性强的方法.例如,矩阵分解方法[13 ] 使用邻接矩阵的近似分解作为嵌入;随机游走法[14 ] 将游走序列输入到Skip-Gram[15 ] 生成嵌入.这些方法利用图的稀疏性降低了时间复杂度.当前,很多综述[16 ,17 ,18 ,19 ,20 ,21 ] 对图嵌入方法进行了归纳与总结,但存在两大局限:一是部分综述仅涉及传统方法介绍,许多新模型没有纳入研究;二是这些综述只关注静态图嵌入或动态图嵌入,忽略了二者之间的关联性. ...
... 许多图分解和重构的目标函数都使用节点向量来确定边的建立.GF(graph factorization)[13 ] 假设边的存在信息可以由节点向量内积 Y i , Y j
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Random walks on graphs: a survey
1
1993
... 早期的图嵌入算法主要用于数据降维,通过邻域关系构建相似度图,将节点嵌入低维向量空间,并保持相连节点向量的相似性.这类方法通常时间复杂度高,很难扩展到大型图上.近年来,图嵌入算法转向扩展性强的方法.例如,矩阵分解方法[13 ] 使用邻接矩阵的近似分解作为嵌入;随机游走法[14 ] 将游走序列输入到Skip-Gram[15 ] 生成嵌入.这些方法利用图的稀疏性降低了时间复杂度.当前,很多综述[16 ,17 ,18 ,19 ,20 ,21 ] 对图嵌入方法进行了归纳与总结,但存在两大局限:一是部分综述仅涉及传统方法介绍,许多新模型没有纳入研究;二是这些综述只关注静态图嵌入或动态图嵌入,忽略了二者之间的关联性. ...
word2vec explained: deriving Mikolov et al.’s negative-sampling word-embedding method
2
2014
... 早期的图嵌入算法主要用于数据降维,通过邻域关系构建相似度图,将节点嵌入低维向量空间,并保持相连节点向量的相似性.这类方法通常时间复杂度高,很难扩展到大型图上.近年来,图嵌入算法转向扩展性强的方法.例如,矩阵分解方法[13 ] 使用邻接矩阵的近似分解作为嵌入;随机游走法[14 ] 将游走序列输入到Skip-Gram[15 ] 生成嵌入.这些方法利用图的稀疏性降低了时间复杂度.当前,很多综述[16 ,17 ,18 ,19 ,20 ,21 ] 对图嵌入方法进行了归纳与总结,但存在两大局限:一是部分综述仅涉及传统方法介绍,许多新模型没有纳入研究;二是这些综述只关注静态图嵌入或动态图嵌入,忽略了二者之间的关联性. ...
... 受word2vec[15 ] 的启发,基于随机游走的图嵌入方法将节点转化为词,将随机游走序列作为句子,利用Skip-Gram生成节点的嵌入向量.随机游走法可以保留图的结构特性,并且在无法完整观察的大型图上仍有不错的表现. ...
A comprehensive survey of graph embedding: problems, techniques, and applications
1
2018
... 早期的图嵌入算法主要用于数据降维,通过邻域关系构建相似度图,将节点嵌入低维向量空间,并保持相连节点向量的相似性.这类方法通常时间复杂度高,很难扩展到大型图上.近年来,图嵌入算法转向扩展性强的方法.例如,矩阵分解方法[13 ] 使用邻接矩阵的近似分解作为嵌入;随机游走法[14 ] 将游走序列输入到Skip-Gram[15 ] 生成嵌入.这些方法利用图的稀疏性降低了时间复杂度.当前,很多综述[16 ,17 ,18 ,19 ,20 ,21 ] 对图嵌入方法进行了归纳与总结,但存在两大局限:一是部分综述仅涉及传统方法介绍,许多新模型没有纳入研究;二是这些综述只关注静态图嵌入或动态图嵌入,忽略了二者之间的关联性. ...
Graph embedding techniques, applications, and performance: a survey
1
2018
... 早期的图嵌入算法主要用于数据降维,通过邻域关系构建相似度图,将节点嵌入低维向量空间,并保持相连节点向量的相似性.这类方法通常时间复杂度高,很难扩展到大型图上.近年来,图嵌入算法转向扩展性强的方法.例如,矩阵分解方法[13 ] 使用邻接矩阵的近似分解作为嵌入;随机游走法[14 ] 将游走序列输入到Skip-Gram[15 ] 生成嵌入.这些方法利用图的稀疏性降低了时间复杂度.当前,很多综述[16 ,17 ,18 ,19 ,20 ,21 ] 对图嵌入方法进行了归纳与总结,但存在两大局限:一是部分综述仅涉及传统方法介绍,许多新模型没有纳入研究;二是这些综述只关注静态图嵌入或动态图嵌入,忽略了二者之间的关联性. ...
Graph repres-entation learning: a survey
1
2020
... 早期的图嵌入算法主要用于数据降维,通过邻域关系构建相似度图,将节点嵌入低维向量空间,并保持相连节点向量的相似性.这类方法通常时间复杂度高,很难扩展到大型图上.近年来,图嵌入算法转向扩展性强的方法.例如,矩阵分解方法[13 ] 使用邻接矩阵的近似分解作为嵌入;随机游走法[14 ] 将游走序列输入到Skip-Gram[15 ] 生成嵌入.这些方法利用图的稀疏性降低了时间复杂度.当前,很多综述[16 ,17 ,18 ,19 ,20 ,21 ] 对图嵌入方法进行了归纳与总结,但存在两大局限:一是部分综述仅涉及传统方法介绍,许多新模型没有纳入研究;二是这些综述只关注静态图嵌入或动态图嵌入,忽略了二者之间的关联性. ...
A survey on network embedding
1
2018
... 早期的图嵌入算法主要用于数据降维,通过邻域关系构建相似度图,将节点嵌入低维向量空间,并保持相连节点向量的相似性.这类方法通常时间复杂度高,很难扩展到大型图上.近年来,图嵌入算法转向扩展性强的方法.例如,矩阵分解方法[13 ] 使用邻接矩阵的近似分解作为嵌入;随机游走法[14 ] 将游走序列输入到Skip-Gram[15 ] 生成嵌入.这些方法利用图的稀疏性降低了时间复杂度.当前,很多综述[16 ,17 ,18 ,19 ,20 ,21 ] 对图嵌入方法进行了归纳与总结,但存在两大局限:一是部分综述仅涉及传统方法介绍,许多新模型没有纳入研究;二是这些综述只关注静态图嵌入或动态图嵌入,忽略了二者之间的关联性. ...
A survey on dynamic network embedding
1
2020
... 早期的图嵌入算法主要用于数据降维,通过邻域关系构建相似度图,将节点嵌入低维向量空间,并保持相连节点向量的相似性.这类方法通常时间复杂度高,很难扩展到大型图上.近年来,图嵌入算法转向扩展性强的方法.例如,矩阵分解方法[13 ] 使用邻接矩阵的近似分解作为嵌入;随机游走法[14 ] 将游走序列输入到Skip-Gram[15 ] 生成嵌入.这些方法利用图的稀疏性降低了时间复杂度.当前,很多综述[16 ,17 ,18 ,19 ,20 ,21 ] 对图嵌入方法进行了归纳与总结,但存在两大局限:一是部分综述仅涉及传统方法介绍,许多新模型没有纳入研究;二是这些综述只关注静态图嵌入或动态图嵌入,忽略了二者之间的关联性. ...
Foundations and modelling of dynamic networks using dynamic graph neural networks: a survey
1
2021
... 早期的图嵌入算法主要用于数据降维,通过邻域关系构建相似度图,将节点嵌入低维向量空间,并保持相连节点向量的相似性.这类方法通常时间复杂度高,很难扩展到大型图上.近年来,图嵌入算法转向扩展性强的方法.例如,矩阵分解方法[13 ] 使用邻接矩阵的近似分解作为嵌入;随机游走法[14 ] 将游走序列输入到Skip-Gram[15 ] 生成嵌入.这些方法利用图的稀疏性降低了时间复杂度.当前,很多综述[16 ,17 ,18 ,19 ,20 ,21 ] 对图嵌入方法进行了归纳与总结,但存在两大局限:一是部分综述仅涉及传统方法介绍,许多新模型没有纳入研究;二是这些综述只关注静态图嵌入或动态图嵌入,忽略了二者之间的关联性. ...
Sparse autoencoder
1
2011
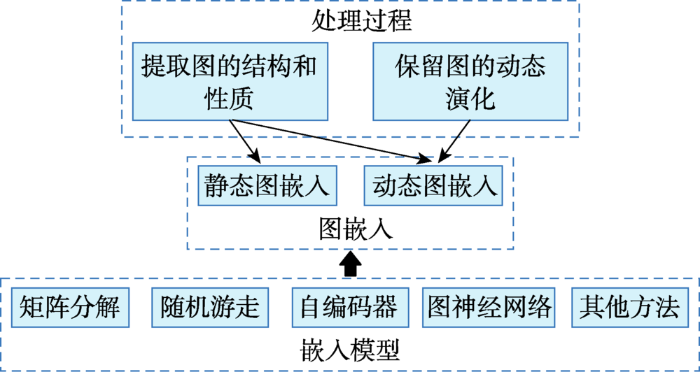
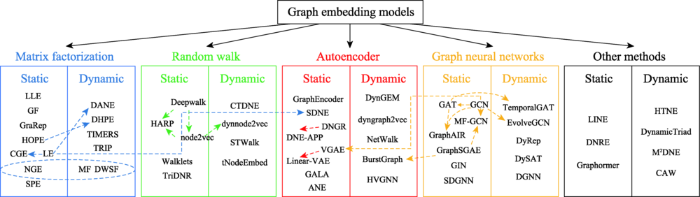
... 本章提出一种新的分类方法,用于现有图嵌入模型的分类.按照模型所使用的算法原理将静态图和动态图模型同时分为五大类:基于矩阵分解的图嵌入、基于随机游走的图嵌入、基于自编码器[22 ] 的图嵌入、基于图神经网络(graph neural networks,GNN)[23 ] 的图嵌入和基于其他方法的图嵌入.图3 为分类思路及内容体系构建,图4 为图嵌入模型的分类汇总. ...
The graph neural network model
1
2008
... 本章提出一种新的分类方法,用于现有图嵌入模型的分类.按照模型所使用的算法原理将静态图和动态图模型同时分为五大类:基于矩阵分解的图嵌入、基于随机游走的图嵌入、基于自编码器[22 ] 的图嵌入、基于图神经网络(graph neural networks,GNN)[23 ] 的图嵌入和基于其他方法的图嵌入.图3 为分类思路及内容体系构建,图4 为图嵌入模型的分类汇总. ...
Nonlinear dimensionality red-uction by locally linear embedding
2
2000
... 局部线性映射(locally linear embedding,LLE)[24 ] 将每个节点表示为相邻节点的线性组合,构造邻域保持映射(见图6 ).具体实现分为三步:(1)以某种度量方式(如欧氏距离)选择k 个邻近节点;(2)由k 个近邻线性加权重构节点,并最小化节点重建误差获得最优权重;(3)最小化最优权重构建的目标函数生成 Y . 目标函数的表达式为: ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
GraRep: learning graph repres-entations with global structural information
2
2015
... GraRep[25 ] 分别构建1到k 步的对数转移概率矩阵 { T 1 , T 2 , ⋯ , T k } , T k T k k 步对数转移概率矩阵,以减少噪声[26 ] .最后,使用SVD分解 T k Y k { Y 1 , Y 2 , ⋯ , Y k } Y . GraRep能够在嵌入中整合全局结构信息,但训练过程中涉及矩阵运算和SVD,计算复杂度极高,难以扩展到大规模图数据. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Neural word embedding as implicit matrix factorization
1
2014
... GraRep[25 ] 分别构建1到k 步的对数转移概率矩阵 { T 1 , T 2 , ⋯ , T k } , T k T k k 步对数转移概率矩阵,以减少噪声[26 ] .最后,使用SVD分解 T k Y k { Y 1 , Y 2 , ⋯ , Y k } Y . GraRep能够在嵌入中整合全局结构信息,但训练过程中涉及矩阵运算和SVD,计算复杂度极高,难以扩展到大规模图数据. ...
Asymmetric transitivity preserving graph embedding
2
2016
... 非对称传递性可以刻画有向边之间的关联,有助于捕捉图的结构.为了保留有向图中的非对称传递性,HOPE[27 ] 采用了一种保持高阶相似度的嵌入方法,在保留非对称传递性的向量空间中生成图嵌入(见图7 ),训练中使用L2范数进行优化: ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
A new status index derived from sociometric analysis
1
1953
... 式中, Y s Y t [28 ] 、Adamic-Adar分数等,用于构建相似度矩阵 S . 此外,HOPE使用广义SVD(generalized singular value decomposition,GSVD)[29 ] 分解 S
Towards a generalized singular value decomposition
1
1981
... 式中, Y s Y t [28 ] 、Adamic-Adar分数等,用于构建相似度矩阵 S . 此外,HOPE使用广义SVD(generalized singular value decomposition,GSVD)[29 ] 分解 S
Non-negative graph embedding
2
2008
... 在原始图上,本征图用于保留节点间有利关联,惩罚图用于保留节点间的不利关联.为了综合本征图和惩罚图的特点,NGE(non-negative graph embedding)[30 ] 引入非负矩阵分解(non-negative matrix factorization,NMF)[31 ] 生成嵌入表示.NMF将数据矩阵分解成低阶非负基矩阵 W Y Y W Y = [ Y 1 , Y 2 ] ; W = [ W 1 , W 2 ] . ( W 1 , Y 1 ) ( W 2 , Y 2 ) Y 2 Y 1 Y 2
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Learning the parts of objects by non-negative matrix factorization
1
1999
... 在原始图上,本征图用于保留节点间有利关联,惩罚图用于保留节点间的不利关联.为了综合本征图和惩罚图的特点,NGE(non-negative graph embedding)[30 ] 引入非负矩阵分解(non-negative matrix factorization,NMF)[31 ] 生成嵌入表示.NMF将数据矩阵分解成低阶非负基矩阵 W Y Y W Y = [ Y 1 , Y 2 ] ; W = [ W 1 , W 2 ] . ( W 1 , Y 1 ) ( W 2 , Y 2 ) Y 2 Y 1 Y 2
Laplacian Eigenmaps and spectral techniques for embedding and clustering
2
2001
... 拉普拉斯特征映射(Laplacian eigenmaps,LE)[32 ] 与LLE相似,也是从局部近似的角度构建数据之间的关系.具体而言,LE使用邻接矩阵建立包含局部结构信息的嵌入表示,并要求相连节点在嵌入空间中尽可能地靠近.因此,LE的目标函数为: ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Cauchy graph embe-dding
2
2011
... 由上式可知,LE的目标函数强调权值大的节点对,弱化权值小的节点对,导致原始图中的局部拓扑结构被破坏.为了增强图嵌入的局部拓扑保持性,柯西图嵌入(Cauchy graph embedding,CGE)[33 ] 引入距离的反函数来保持节点在嵌入空间中的相似关系.因此,CGE将LE的目标函数改写为: ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Structure preserving embedding
2
2009
... 为了保持图的全局拓扑结构,SPE(structure preserving embedding)[34 ] 通过一组线性不等式学习包含节点连接关系的低阶核矩阵获得嵌入表示.SPE以核矩阵 K f 输出关系矩阵 A ˜ = f ( K ) . 通过比较邻接矩阵 A A ˜ K
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
1
2013
... 从矩阵分解的角度看,图的动态演化实质上是原始矩阵的不断变化.基于矩阵分解的动态图方法利用特征分解构造图的高阶相似度矩阵,然后利用矩阵摄动理论[35 ] 更新图的动态信息.矩阵摄动理论可以高效更新图的高级特征对,同时避免了每个时刻的重新计算嵌入矩阵.图8 是基于矩阵分解的动态图嵌入的一般过程. ...
Attributed network embe-dding for learning in a dynamic environment
2
2017
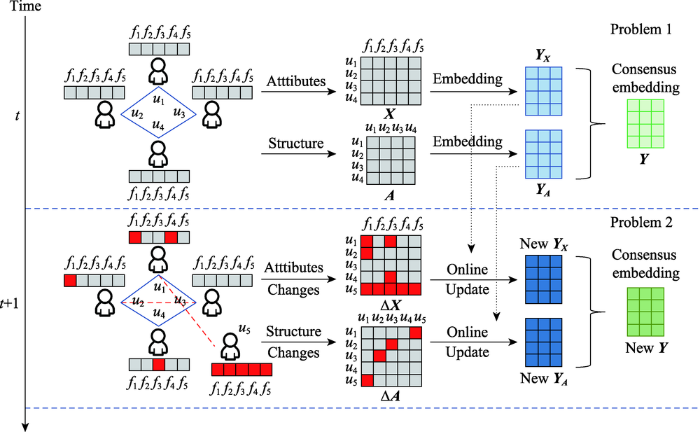
... DANE[36 ] 采用分布式框架(见图9 ):离线部分,采用最大化相关性[37 ] 的方法,引入 p A t p X t Y A t Y X t d Y A t Y X t t t + 1 Y A Y X
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Canonical correlation analysis: an overview with application to learning methods
1
2004
... DANE[36 ] 采用分布式框架(见图9 ):离线部分,采用最大化相关性[37 ] 的方法,引入 p A t p X t Y A t Y X t d Y A t Y X t t t + 1 Y A Y X
High-order proximity preserved embedding for dynamic networks
2
2018
... DHPE[38 ] 同样采用分布式框架:静态部分,DHPE与HOPE相似,将GSVD分解Katz相似度矩阵转换为广义特征值问题[39 ] ,使每个时刻生成的低维嵌入保留节点的高阶相似度;动态部分,DHPE使用矩阵摄动理论更新GSVD的结果.此外,模型假设图中节点数恒定(添加或删除的节点为孤立节点),使每个时刻图的变化转化为边的变化.DHPE能够在保持高阶相似性的同时更新节点嵌入,其增量计算方案有效提升了动态模型的计算效率. ...
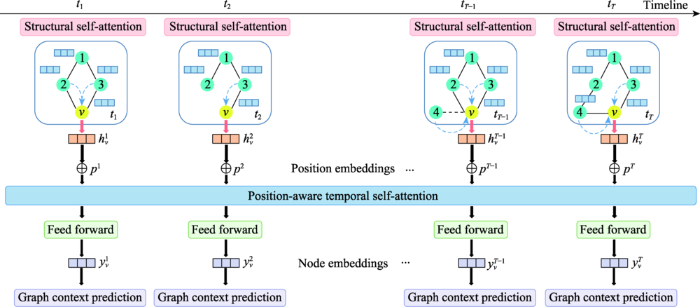
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
1
1993
... DHPE[38 ] 同样采用分布式框架:静态部分,DHPE与HOPE相似,将GSVD分解Katz相似度矩阵转换为广义特征值问题[39 ] ,使每个时刻生成的低维嵌入保留节点的高阶相似度;动态部分,DHPE使用矩阵摄动理论更新GSVD的结果.此外,模型假设图中节点数恒定(添加或删除的节点为孤立节点),使每个时刻图的变化转化为边的变化.DHPE能够在保持高阶相似性的同时更新节点嵌入,其增量计算方案有效提升了动态模型的计算效率. ...
Fast Eigen-functions tracking on dynamic graphs
2
2015
... Chen等人[40 ] 提出了TRIP和TRIP-BASIC两种在线算法跟踪动态图的特征对,其核心思路是利用矩阵摄动理论对图的特征对进行更新.TRIP和TRIP-BASIC引入图中三角形个数[41 ,42 ] 作为属性信息构建特征函数,然后将特征对映射成属性向量.上述模型能够有效追踪特征对、三角形个数和鲁棒性分数随时间的动态变化,但是模型的误差会随着时间推移不断积累. ...
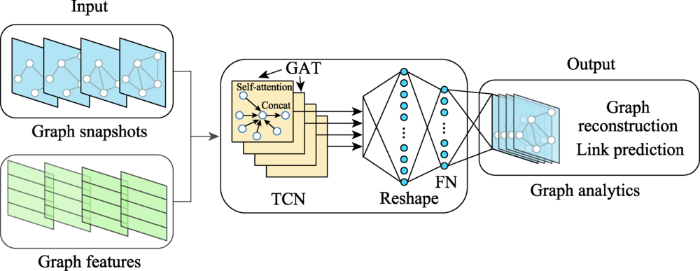
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Fast counting of triangles in large real networks without counting: algorithms and laws
2
2008
... Chen等人[40 ] 提出了TRIP和TRIP-BASIC两种在线算法跟踪动态图的特征对,其核心思路是利用矩阵摄动理论对图的特征对进行更新.TRIP和TRIP-BASIC引入图中三角形个数[41 ,42 ] 作为属性信息构建特征函数,然后将特征对映射成属性向量.上述模型能够有效追踪特征对、三角形个数和鲁棒性分数随时间的动态变化,但是模型的误差会随着时间推移不断积累. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Counting triangles in real-world networks using projections
1
2011
... Chen等人[40 ] 提出了TRIP和TRIP-BASIC两种在线算法跟踪动态图的特征对,其核心思路是利用矩阵摄动理论对图的特征对进行更新.TRIP和TRIP-BASIC引入图中三角形个数[41 ,42 ] 作为属性信息构建特征函数,然后将特征对映射成属性向量.上述模型能够有效追踪特征对、三角形个数和鲁棒性分数随时间的动态变化,但是模型的误差会随着时间推移不断积累. ...
Timers: error-bounded SVD restart on dynamic networks
1
2018
... 由于增量矩阵的更新采用近似值的方式,导致生成嵌入的过程中误差不断积累.为解决上述问题,TIMERS[43 ] 采用SVD最大误差界重启算法,设置SVD重新启动时间,减少时间上的误差积累.该模型的核心包含两部分:(1)增量更新,通过函数f 近似地更新前一时刻的结果;(2)SVD重启,通过设置误差阈值,确定执行SVD重启时刻,重新计算最优SVD结果,并最小化重启次数. ...
DeepEye: link prediction in dynamic networks based on non-negative matrix factorization
1
2018
... MF[44 ] 通过构造携带重要特征的矩阵因子,使潜在的NMF特征有效地表达动态信息.为了充分利用不同时刻的拓扑信息,MF对嵌入空间的邻接关系矩阵进行整合,找到在各个时刻一致的嵌入矩阵 Y * W * Y t Y * W t W *
A weakly-supervised factorization method with dynamic graph embedding
2
2017
... DWSF[45 ] 采用使用Semi-NMF[46 ] 和弱监督分解(weakly supervised factorization,WSF)[47 ] ,将数据矩阵 X M Y ( X = MY , M X Y [48 ] 初始化标签矩阵因子,将类标签从有标签的数据实例传播到无标签的数据实例,最后将控制信息量的平滑度项与Semi-NMF相结合,优化模型参数生成嵌入.DWSF将有限的监督信息合并为类别标签,在每次迭代中动态更新,大幅提升了模型在分类任务上的表现. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Nonnegative matrix factorization: a comprehensive review
1
2012
... DWSF[45 ] 采用使用Semi-NMF[46 ] 和弱监督分解(weakly supervised factorization,WSF)[47 ] ,将数据矩阵 X M Y ( X = MY , M X Y [48 ] 初始化标签矩阵因子,将类标签从有标签的数据实例传播到无标签的数据实例,最后将控制信息量的平滑度项与Semi-NMF相结合,优化模型参数生成嵌入.DWSF将有限的监督信息合并为类别标签,在每次迭代中动态更新,大幅提升了模型在分类任务上的表现. ...
A deep matrix factorization method for learning attribute representations
1
2016
... DWSF[45 ] 采用使用Semi-NMF[46 ] 和弱监督分解(weakly supervised factorization,WSF)[47 ] ,将数据矩阵 X M Y ( X = MY , M X Y [48 ] 初始化标签矩阵因子,将类标签从有标签的数据实例传播到无标签的数据实例,最后将控制信息量的平滑度项与Semi-NMF相结合,优化模型参数生成嵌入.DWSF将有限的监督信息合并为类别标签,在每次迭代中动态更新,大幅提升了模型在分类任务上的表现. ...
Learning to propagate labels: transductive propagation network for few-shot learning
1
2018
... DWSF[45 ] 采用使用Semi-NMF[46 ] 和弱监督分解(weakly supervised factorization,WSF)[47 ] ,将数据矩阵 X M Y ( X = MY , M X Y [48 ] 初始化标签矩阵因子,将类标签从有标签的数据实例传播到无标签的数据实例,最后将控制信息量的平滑度项与Semi-NMF相结合,优化模型参数生成嵌入.DWSF将有限的监督信息合并为类别标签,在每次迭代中动态更新,大幅提升了模型在分类任务上的表现. ...
DeepWalk: online learning of social representations
2
2014
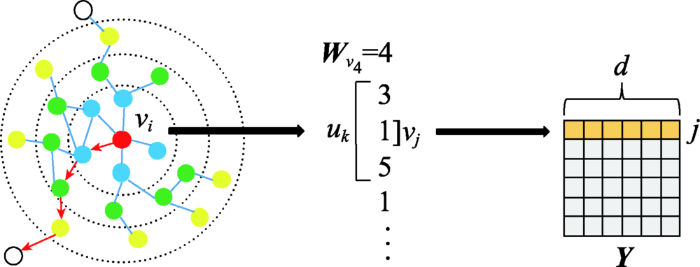
... Deepwalk[49 ] 使用随机游走对节点进行采样,生成节点序列,再通过Skip-Gram最大化节点序列中窗口 w v j Y j 图10 ): ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
node2vec: scalable feature learning for networks
2
2016
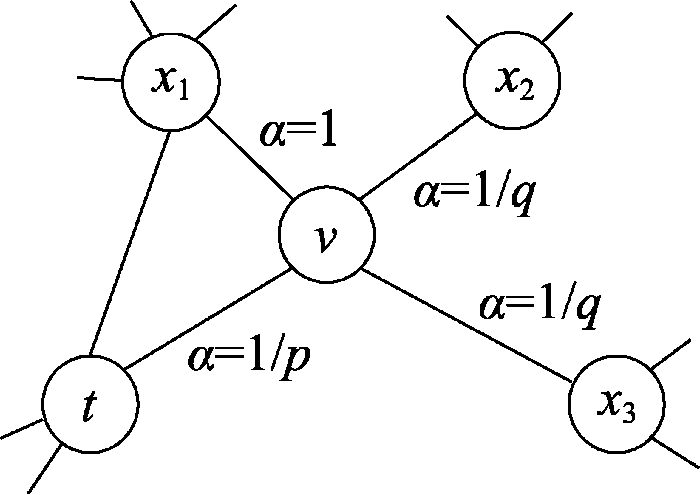
... node2vec[50 ] 在Deepwalk的基础上,引入有偏的随机游走(见图11 ),增加邻域搜索的灵活性,生成质量更高、信息更多的嵌入表示.通过设置 p q
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Harp: hierarchical representation learning for networks
2
2018
... Deepwalk和node2vec采用随机游走探索节点局部邻域,使得学习到的低维表示无法保留图的全局结构,同时使用随机梯度下降求解非凸的目标函数,使生成的嵌入可能陷入局部最优解.为了解决上述问题,HARP[51 ] 将原始图中的节点和边递归地合并在一起,得到一系列结构相似的压缩图.这些压缩图有不同的粒度,提供了原始图全局结构的视图.从最粗略的形式开始,每个压缩图学习一组嵌入表示,并用于初始化下一个更细化的压缩图的嵌入.HARP能够与Deepwalk和node2vec结合使用,提升原始模型性能,生成信息更丰富的嵌入表示. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Comprehend deepwalk as matrix factor-ization
2
2015
... 利用分层Softmax,Deepwalk目标函数可以改写为矩阵分解的形式[52 ] : ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Walklets: multiscale graph embeddings for interpretable network classification
2
2016
... 式中, M ij i j k e i i A k k k 阶关系,Walklets[53 ] 修改了Deepwalk的采样过程,在随机游走序列上跳过 k - 1
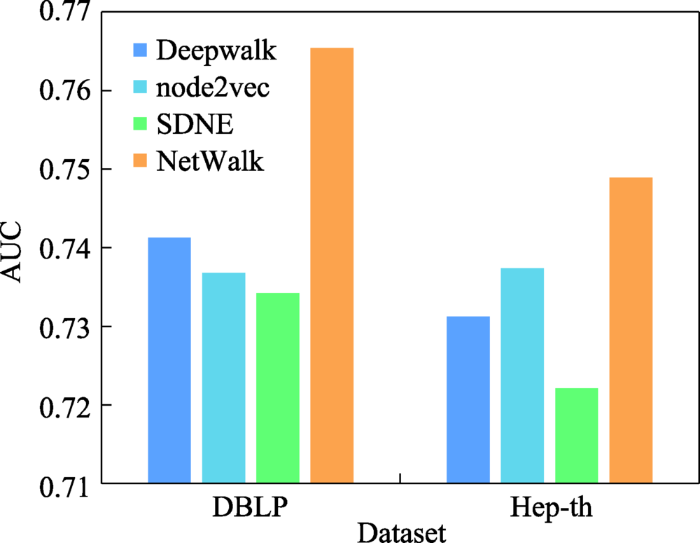
... DBLP[53 ] :引文网络数据集,每个顶点表示一个作者,从一个作者到另一个作者的参考文献数量由这两个作者之间的边权重来记录.标签上标明了研究人员发表研究成果的4个领域. ...
Tri-party deep network representation
2
2016
... TriDNR[54 ] 是首个利用标签信息进行表示学习的深层神经网络模型,能够同时利用网络结构、节点特征和节点标签学习节点嵌入表示(见图12 ).具体而言,TriDNR使用两个神经网络来捕获节点-节点、节点-单词、标签-单词之间的关系.对于网络结构,通过随机游走序列最大化共现概率来保持图中节点间的邻近关系;对于节点特征,通过最大化给定节点的单词序列的共现概率捕获节点与单词的相关性;对于节点标签,通过最大化给定类别标签的单词序列的概率建模标签与单词的对应关系.最后,使用耦合神经网络的算法将三部分信息合并为节点嵌入. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Efficient representation learning using random walks for dynamic graphs
1
2019
... Sajjad等人[55 ] 将图嵌入的生成过程分为两步:首先,更新动态图上的随机游走序列.与直接在静态快照上从头开始随机游走相比,更新算法保持了随机游走的统计特性.然后,在给定前一时刻的嵌入表示以及更新后的随机游走序列的条件下,利用Skip-Gram模型对嵌入表示进行更新.CTDNE[56 ] 则利用时间随机游走从连续型动态图中学习包含时间信息的嵌入表示.实际上,CTDNE采用的时间随机游走与静态图方法相似,但约束每个随机游走符合边出现的时间顺序,即边的遍历必须按照时间递增的顺序,由于每条边包含多个时间戳,使得同一节点可能在游走中出现多次.时间信息的引入减少了嵌入的不确定性,使CTDNE在众多任务上的表现优于Deepwalk和node2vec等静态模型. ...
Continuous-time dynamic network embeddings
2
2018
... Sajjad等人[55 ] 将图嵌入的生成过程分为两步:首先,更新动态图上的随机游走序列.与直接在静态快照上从头开始随机游走相比,更新算法保持了随机游走的统计特性.然后,在给定前一时刻的嵌入表示以及更新后的随机游走序列的条件下,利用Skip-Gram模型对嵌入表示进行更新.CTDNE[56 ] 则利用时间随机游走从连续型动态图中学习包含时间信息的嵌入表示.实际上,CTDNE采用的时间随机游走与静态图方法相似,但约束每个随机游走符合边出现的时间顺序,即边的遍历必须按照时间递增的顺序,由于每条边包含多个时间戳,使得同一节点可能在游走中出现多次.时间信息的引入减少了嵌入的不确定性,使CTDNE在众多任务上的表现优于Deepwalk和node2vec等静态模型. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Dynnode2vec: scalable dynamic network embedding
2
2018
... 在动态图中应用静态方法存在两大问题:(1)对每个快照都进行随机游走非常耗时;(2)不同快照的嵌入空间并不一致.为解决上述问题,Mahdavi等人在node2vec的基础上,提出了动态图嵌入模型dynnode2vec[57 ] .该模型在快照G 1 上运行node2vec获得嵌入向量以及训练后的Skip-Gram模型.对于后续快照,在两个连续快照之间执行以下步骤:(1)为演化节点生成随机游走序列;(2)使用动态Skip-Gram[58 ] 将前一时刻学习到的嵌入作为初始权值,结合演化节点的随机游走生成当前时刻嵌入.由于动态图是逐渐演化的,即大多数节点的邻域保持不变,dynnode2vec仅对演化节点进行随机游走大幅提升了模型效率. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Temporal analysis of language through neural language models
1
2014
... 在动态图中应用静态方法存在两大问题:(1)对每个快照都进行随机游走非常耗时;(2)不同快照的嵌入空间并不一致.为解决上述问题,Mahdavi等人在node2vec的基础上,提出了动态图嵌入模型dynnode2vec[57 ] .该模型在快照G 1 上运行node2vec获得嵌入向量以及训练后的Skip-Gram模型.对于后续快照,在两个连续快照之间执行以下步骤:(1)为演化节点生成随机游走序列;(2)使用动态Skip-Gram[58 ] 将前一时刻学习到的嵌入作为初始权值,结合演化节点的随机游走生成当前时刻嵌入.由于动态图是逐渐演化的,即大多数节点的邻域保持不变,dynnode2vec仅对演化节点进行随机游走大幅提升了模型效率. ...
STWalk: learning trajectory representations in temporal graphs
2
2018
... STWalk[59 ] 是一种无监督节点轨迹学习算法,通过捕捉给定时间窗口内节点变化生成嵌入表示.该模型将当前时刻快照上的随机游走定义为空间游走,过去时刻快照上的随机游走定义为时间游走,从而捕捉节点的时空行为,然后利用Skip-Gram生成节点轨迹的嵌入表示.STWalk有两种不同的变体:STWalk1同时考虑空间游走和时间游走来学习嵌入表示;STWalk2将空间游走和时间游走建模为两个子问题并分别求解,然后组合两个结果获得最终的嵌入表示.上述模型仅使用图的结构信息学习捕获节点轨迹时空特性的低维嵌入,未考虑节点特征和标签信息. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Node embedding over temporal graphs
2
2019
... Deepwalk和node2vec模仿单词嵌入作为节点嵌入表示,而tNodeEmbed[60 ] 模仿句子嵌入[61 ] 作为节点嵌入表示.句子中每个单词不仅代表节点随时间变化的向量,还捕捉了节点角色和连接关系的动态变化.为此,tNodeEmbed使用联合损失函数优化两个目标:(1)三维特征空间中节点的静态邻域;(2)图的动态特性.tNodeEmbed使用node2vec对节点嵌入进行初始化,将不同时刻的节点表示进行对齐,然后根据给定的图分析任务和过去时刻的节点嵌入联合学习,使生成的嵌入既保留图的结构和动态信息,又适用于特定任务. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Deep sentence embedding using the long short term memory network: analysis and application to information retrieval
1
2015
... Deepwalk和node2vec模仿单词嵌入作为节点嵌入表示,而tNodeEmbed[60 ] 模仿句子嵌入[61 ] 作为节点嵌入表示.句子中每个单词不仅代表节点随时间变化的向量,还捕捉了节点角色和连接关系的动态变化.为此,tNodeEmbed使用联合损失函数优化两个目标:(1)三维特征空间中节点的静态邻域;(2)图的动态特性.tNodeEmbed使用node2vec对节点嵌入进行初始化,将不同时刻的节点表示进行对齐,然后根据给定的图分析任务和过去时刻的节点嵌入联合学习,使生成的嵌入既保留图的结构和动态信息,又适用于特定任务. ...
Auto-association by multilayer perceptrons and singular value decomposition
1
1988
... 自编码器(autoencoder,AE)[62 ] 是一种人工神经网络,包含编码器和解码器两部分,用于无监督地构造输入数据的向量表示.通过对数据中的非线性结构进行建模,自编码器使隐藏层学习到的表示维度小于输入数据,即对原始数据进行降维.基于自编码器的图嵌入方法使用自编码器对图的非线性结构建模,生成图的低维嵌入表示. ...
Learning deep representations for graph clustering
3
2014
... 基于自编码器的图嵌入方法起源于使用稀疏自编码器的GraphEncoder[63 ] .其基本思想是将归一化的图相似度矩阵作为节点原始特征输入到稀疏自编码器中进行分层预训练,使生成的低维非线性嵌入可以近似地重建输入矩阵并保留稀疏特性: ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
... 20-Newsgroup[63 ] :由大约20 000个新闻组文档构成的数据集.这些文档根据主题划分成20个组,每个文档表示为每个词的TF-IDF分数向量,构建余弦相似图.为了证明聚类算法的稳健性,分别从3、6和9个不同的新闻组构建了3个图,使用的缩写NG是Newsgroup的缩写. ...
Structural deep network embedding
2
2016
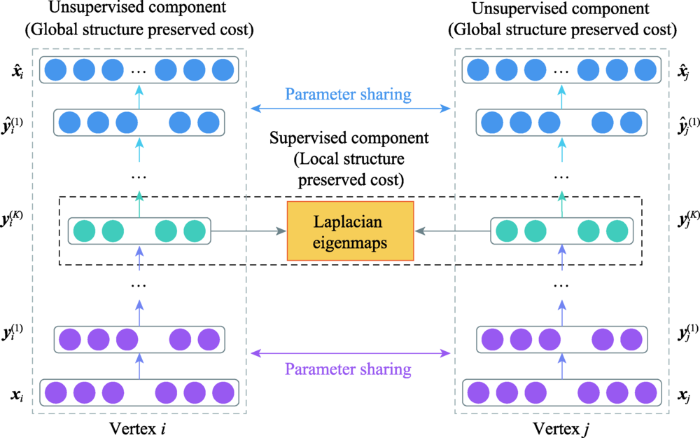
... SDNE[64 ] 利用深度自编码器以及图的一阶、二阶相似度,捕获高度非线性的网络结构.SDNE包含有监督组件和无监督组件(见图13 ),用于保持节点的一阶和二阶相似度.有监督组件引入拉普拉斯特征映射作为一阶相似度的目标函数,使生成的嵌入捕获局部结构信息.无监督组件修改L2重建损失函数作为二阶相似度的目标函数,使生成的嵌入捕获全局结构信息.对一阶和二阶相似度联合优化,增强了模型在稀疏图上的鲁棒性,使生成的嵌入同时保留全局和局部结构信息. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Deep neural networks for learning graph representations
2
2016
... DNGR[65 ] 生成低维嵌入的过程主要分为三步:(1)利用随机冲浪模型捕捉图的结构信息,并生成共现概率矩阵;(2)利用共现概率矩阵计算正逐点互信息(positive pointwise mutual information,PPMI)矩阵[66 ] ;(3)将PPMI矩阵输入堆叠去噪自编码器(stacked denoising autoencoder,SDAE)生成低维嵌入表示.相较于随机游走,随机冲浪直接获取图的结构信息,克服了原有采样过程的限制;PPMI矩阵能够保留图的高阶相似度信息;堆叠结构使隐层维度平滑递减,提升深层架构学习复杂特征的能力,同时去噪策略增强了模型的鲁棒性. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Extracting semantic repres-entations from word co-occurrence statistics: a computational study
1
2007
... DNGR[65 ] 生成低维嵌入的过程主要分为三步:(1)利用随机冲浪模型捕捉图的结构信息,并生成共现概率矩阵;(2)利用共现概率矩阵计算正逐点互信息(positive pointwise mutual information,PPMI)矩阵[66 ] ;(3)将PPMI矩阵输入堆叠去噪自编码器(stacked denoising autoencoder,SDAE)生成低维嵌入表示.相较于随机游走,随机冲浪直接获取图的结构信息,克服了原有采样过程的限制;PPMI矩阵能够保留图的高阶相似度信息;堆叠结构使隐层维度平滑递减,提升深层架构学习复杂特征的能力,同时去噪策略增强了模型的鲁棒性. ...
Deep network embedding with aggregated proximity preserving
2
2017
... DNE-APP[67 ] 利用半监督堆叠式自编码器(stacked autoencoder,SAE)生成保留k 阶信息的低维嵌入主要分为两步:(1)使用PPMI度量和k 步转移概率矩阵,生成包含k 阶信息的相似度聚合矩阵.(2)使用SAE重构相似度聚合矩阵,学习低维非线性嵌入表示.与仅保持一阶和二阶相似度的SDNE相比,DNE-APP模型可以保持不同的k 阶相似度;与仅重建高阶相似度的DNGR相比,DNE-APP在重建过程中引入了成对约束,使相似节点在嵌入空间更加接近. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Auto-encoding variational Bayes
1
2013
... 变分自编码器(variational autoencoder,VAE)[68 ] 是用于降维的生成式模型,其优势为容忍噪声和学习平滑的表示.VGAE[69 ] 首先引入VAE学习可解释的无向图嵌入表示.模型的编码器部分使用图卷积网络(graph convolutional network,GCN)[70 ] : ...
Variational graph auto-encoders
2
2016
... 变分自编码器(variational autoencoder,VAE)[68 ] 是用于降维的生成式模型,其优势为容忍噪声和学习平滑的表示.VGAE[69 ] 首先引入VAE学习可解释的无向图嵌入表示.模型的编码器部分使用图卷积网络(graph convolutional network,GCN)[70 ] : ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Semi-supervised classification with graph convolutional networks
2
2016
... 变分自编码器(variational autoencoder,VAE)[68 ] 是用于降维的生成式模型,其优势为容忍噪声和学习平滑的表示.VGAE[69 ] 首先引入VAE学习可解释的无向图嵌入表示.模型的编码器部分使用图卷积网络(graph convolutional network,GCN)[70 ] : ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
On information and suffi-ciency
1
1951
... 式中, KL [ q ( · ) | | p ( · ) ] q ( · ) p ( · ) KL [71 ] , p ( Y )
Keep it simple: graph autoencoders without graph convolutional networks
1
2019
... Salha等人提出的Linear-VGAE模型[72 ] 使用基于归一化邻接矩阵的简单线性模型替换VGAE中的GCN编码器: ...
Symmetric graph convolutional autoencoder for unsupervised graph represen-tation learning
2
2019
... 与一般的非对称模型不同,GALA[73 ] 采用完全对称的图卷积自编码器模型生成图的低维嵌入表示.在对输入矩阵重构的过程中,编码器执行的拉普拉斯平滑[74 ] 与解码器的拉普拉斯锐化[75 ] 相对称.与现有的VGAE方法不同,为了使解码器可以直接重构节点的特征矩阵,GALA使用谱半径为1的拉普拉斯锐化表示.相较于仅使用GCN编码器的模型,GALA的对称结构,能够在编码和解码过程中同时使用结构信息和节点特征. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Learning a spatially smooth subspace for face recognition
1
2007
... 与一般的非对称模型不同,GALA[73 ] 采用完全对称的图卷积自编码器模型生成图的低维嵌入表示.在对输入矩阵重构的过程中,编码器执行的拉普拉斯平滑[74 ] 与解码器的拉普拉斯锐化[75 ] 相对称.与现有的VGAE方法不同,为了使解码器可以直接重构节点的特征矩阵,GALA使用谱半径为1的拉普拉斯锐化表示.相较于仅使用GCN编码器的模型,GALA的对称结构,能够在编码和解码过程中同时使用结构信息和节点特征. ...
A signal processing approach to fair surface design
1
1995
... 与一般的非对称模型不同,GALA[73 ] 采用完全对称的图卷积自编码器模型生成图的低维嵌入表示.在对输入矩阵重构的过程中,编码器执行的拉普拉斯平滑[74 ] 与解码器的拉普拉斯锐化[75 ] 相对称.与现有的VGAE方法不同,为了使解码器可以直接重构节点的特征矩阵,GALA使用谱半径为1的拉普拉斯锐化表示.相较于仅使用GCN编码器的模型,GALA的对称结构,能够在编码和解码过程中同时使用结构信息和节点特征. ...
ANE: network embe-dding via adversarial autoencoders
2
2018
... ANE[76 ] 使用对抗性自编码器[77 ] 生成捕获高度非线性结构信息的低维嵌入.具体而言,ANE利用一阶和二阶相似度捕捉图的局部和全局结构,使生成的嵌入可以保持高度的非线性,同时训练过程对抗性自编码器的两个准则:一是基于重建误差的自编码器训练准则;二是将嵌入表示的聚合后验分布与任意先验分布匹配的对抗性训练准则.通过施加对抗性正则化,ANE改善了嵌入生成过程中的流形断裂问题,提升了低维嵌入的表示能力. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Adversarial autoencoders
1
2015
... ANE[76 ] 使用对抗性自编码器[77 ] 生成捕获高度非线性结构信息的低维嵌入.具体而言,ANE利用一阶和二阶相似度捕捉图的局部和全局结构,使生成的嵌入可以保持高度的非线性,同时训练过程对抗性自编码器的两个准则:一是基于重建误差的自编码器训练准则;二是将嵌入表示的聚合后验分布与任意先验分布匹配的对抗性训练准则.通过施加对抗性正则化,ANE改善了嵌入生成过程中的流形断裂问题,提升了低维嵌入的表示能力. ...
DynGEM: deep embedding method for dynamic graphs
2
2018
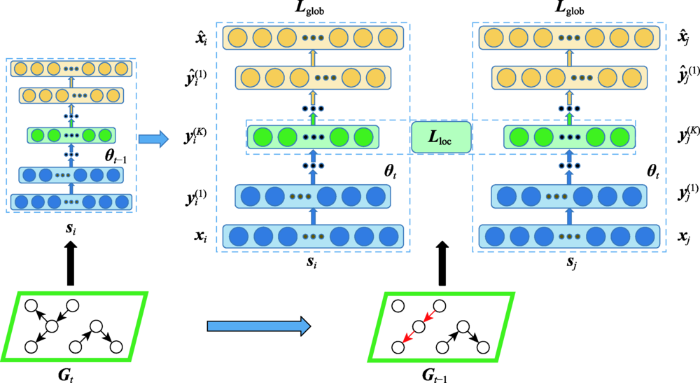
... 受SDNE的启发,Goyal等人提出了快照型动态图嵌入模型DynGEM[78 ] (见图14 ).该模型使用深度自编码器将输入数据映射到高度非线性的低维嵌入空间,以捕捉任一时刻快照中节点的连接趋势,同时下一个时刻的嵌入模型直接继承前一个时刻的训练参数,使t 时刻的快照嵌入可以利用 t - 1 f t - 1 f t
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Dyngraph2vec: capturing network dynamics using dynamic graph repres-entation learning
2
2020
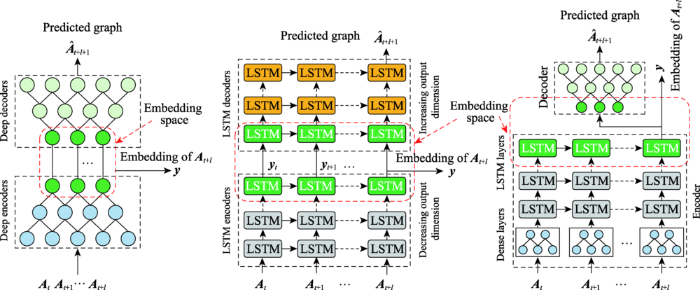
... DynGEM生成当前时刻嵌入时只捕获了前一时刻的信息,致使大量历史信息被忽略,为此Goyal等人提出了另一个基于自编码器的动态图嵌入模型dyngraph2vec[79 ] .该模型将之前l 个时刻的图结构信息作为输入,将当前时刻生成图嵌入作为输出,从而捕获当前时刻与之前多个时刻节点之间的非线性交互信息.该模型有三种变体(见图15 ):dyngraph-2vecAE以一种简单的方式对自编码器进行扩展;dyngraph2vecRNN和dyngraph2vecAERNN使用长短期记忆网络(long short-term memory,LSTM)[80 ] 对历史信息编码.在动态图的演化过程中,dyngraph2vec仅使用相邻节点,未考虑图的高阶相似度信息. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Long short-term memory
1
1997
... DynGEM生成当前时刻嵌入时只捕获了前一时刻的信息,致使大量历史信息被忽略,为此Goyal等人提出了另一个基于自编码器的动态图嵌入模型dyngraph2vec[79 ] .该模型将之前l 个时刻的图结构信息作为输入,将当前时刻生成图嵌入作为输出,从而捕获当前时刻与之前多个时刻节点之间的非线性交互信息.该模型有三种变体(见图15 ):dyngraph-2vecAE以一种简单的方式对自编码器进行扩展;dyngraph2vecRNN和dyngraph2vecAERNN使用长短期记忆网络(long short-term memory,LSTM)[80 ] 对历史信息编码.在动态图的演化过程中,dyngraph2vec仅使用相邻节点,未考虑图的高阶相似度信息. ...
NetWalk: a flexible deep embedding approach for anomaly detection in dynamic networks
2
2018
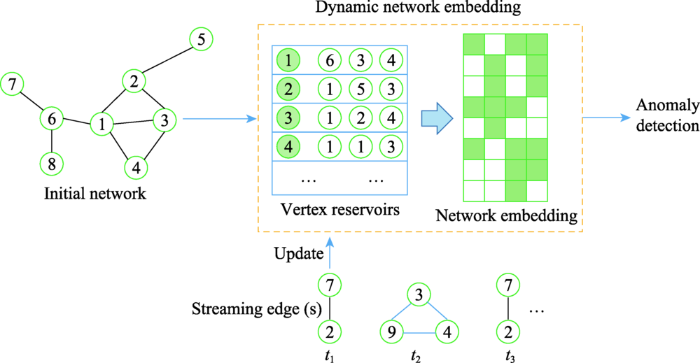
... 随着动态图的演化,NetWalk[81 ] 可以增量地学习网络表示(见图16 ).具体而言,NetWalk利用初始的动态图上提取的多个游走序列以及深度自编码器的隐藏层生成节点嵌入表示.在训练过程中,NetWalk联合最小化游走序列中成对节点的表示距离和自编码器的重构误差,使学习到的嵌入表示既可以实现局部拟合,又可以实现全局正则化.NetWalk对生成到的嵌入表示使用动态聚类模型,能够标记图中异常[82 ,83 ] 的节点或边. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Anomaly, event, and fraud detection in large network datasets
1
2013
... 随着动态图的演化,NetWalk[81 ] 可以增量地学习网络表示(见图16 ).具体而言,NetWalk利用初始的动态图上提取的多个游走序列以及深度自编码器的隐藏层生成节点嵌入表示.在训练过程中,NetWalk联合最小化游走序列中成对节点的表示距离和自编码器的重构误差,使学习到的嵌入表示既可以实现局部拟合,又可以实现全局正则化.NetWalk对生成到的嵌入表示使用动态聚类模型,能够标记图中异常[82 ,83 ] 的节点或边. ...
Graph based anomaly detection and description: a survey
1
2015
... 随着动态图的演化,NetWalk[81 ] 可以增量地学习网络表示(见图16 ).具体而言,NetWalk利用初始的动态图上提取的多个游走序列以及深度自编码器的隐藏层生成节点嵌入表示.在训练过程中,NetWalk联合最小化游走序列中成对节点的表示距离和自编码器的重构误差,使学习到的嵌入表示既可以实现局部拟合,又可以实现全局正则化.NetWalk对生成到的嵌入表示使用动态聚类模型,能够标记图中异常[82 ,83 ] 的节点或边. ...
Large scale evolving graphs with burst detection
2
2019
... BurstGraph[84 ] 将动态图的演化分为一般演化和突发演化,并使用两个基于RNN的VAE分别对每个时刻的演化信息进行建模.在编码器部分,两个自编码器共同使用GraphSAGE[85 ] 学习到的节点特征和拓扑结构信息.对于突发演化,BurstGraph在VAE中引入了spike & slab分布[86 ] 作为近似后验分布;对于一般演化,BurstGraph使用原始的VAE模型.为了充分利用图的动态信息,BurstGraph使用RNN捕捉每个时刻的图结构,将一般演化和突发演化信息保留在RNN状态单元中,并随时间的推移不断更新状态单元.由于生成的嵌入中保留了突发信息,BurstGraph常用于关于图的异常检测中的突发检测[87 ,88 ] 任务. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Inductive representation learning on large graphs
2
2017
... BurstGraph[84 ] 将动态图的演化分为一般演化和突发演化,并使用两个基于RNN的VAE分别对每个时刻的演化信息进行建模.在编码器部分,两个自编码器共同使用GraphSAGE[85 ] 学习到的节点特征和拓扑结构信息.对于突发演化,BurstGraph在VAE中引入了spike & slab分布[86 ] 作为近似后验分布;对于一般演化,BurstGraph使用原始的VAE模型.为了充分利用图的动态信息,BurstGraph使用RNN捕捉每个时刻的图结构,将一般演化和突发演化信息保留在RNN状态单元中,并随时间的推移不断更新状态单元.由于生成的嵌入中保留了突发信息,BurstGraph常用于关于图的异常检测中的突发检测[87 ,88 ] 任务. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Bayesian variable selection in linear regression
1
1988
... BurstGraph[84 ] 将动态图的演化分为一般演化和突发演化,并使用两个基于RNN的VAE分别对每个时刻的演化信息进行建模.在编码器部分,两个自编码器共同使用GraphSAGE[85 ] 学习到的节点特征和拓扑结构信息.对于突发演化,BurstGraph在VAE中引入了spike & slab分布[86 ] 作为近似后验分布;对于一般演化,BurstGraph使用原始的VAE模型.为了充分利用图的动态信息,BurstGraph使用RNN捕捉每个时刻的图结构,将一般演化和突发演化信息保留在RNN状态单元中,并随时间的推移不断更新状态单元.由于生成的嵌入中保留了突发信息,BurstGraph常用于关于图的异常检测中的突发检测[87 ,88 ] 任务. ...
Bayesian anomaly detection methods for social networks
1
2010
... BurstGraph[84 ] 将动态图的演化分为一般演化和突发演化,并使用两个基于RNN的VAE分别对每个时刻的演化信息进行建模.在编码器部分,两个自编码器共同使用GraphSAGE[85 ] 学习到的节点特征和拓扑结构信息.对于突发演化,BurstGraph在VAE中引入了spike & slab分布[86 ] 作为近似后验分布;对于一般演化,BurstGraph使用原始的VAE模型.为了充分利用图的动态信息,BurstGraph使用RNN捕捉每个时刻的图结构,将一般演化和突发演化信息保留在RNN状态单元中,并随时间的推移不断更新状态单元.由于生成的嵌入中保留了突发信息,BurstGraph常用于关于图的异常检测中的突发检测[87 ,88 ] 任务. ...
Bursty and hierarchical structure in streams
1
2003
... BurstGraph[84 ] 将动态图的演化分为一般演化和突发演化,并使用两个基于RNN的VAE分别对每个时刻的演化信息进行建模.在编码器部分,两个自编码器共同使用GraphSAGE[85 ] 学习到的节点特征和拓扑结构信息.对于突发演化,BurstGraph在VAE中引入了spike & slab分布[86 ] 作为近似后验分布;对于一般演化,BurstGraph使用原始的VAE模型.为了充分利用图的动态信息,BurstGraph使用RNN捕捉每个时刻的图结构,将一般演化和突发演化信息保留在RNN状态单元中,并随时间的推移不断更新状态单元.由于生成的嵌入中保留了突发信息,BurstGraph常用于关于图的异常检测中的突发检测[87 ,88 ] 任务. ...
On the hyperbolicity of small-world and treelike random graphs
1
2013
... 动态图嵌入通常存在三方面的局限性:(1)嵌入表示空间[89 ,90 ] ,欧式空间表示可能导致图的潜在层次结构失真;(2)动态信息,忽视图的动态演化通常会导致模型错误地利用未来信息来预测过去的交互;(3)不确定性[91 ] ,图的固有特性,生成的确定性表示不能对不确定性建模.为了解决上述问题,HVGNN[92 ] 采用双曲变分GNN对双曲空间中的动态图进行建模,使生成的嵌入同时包含图的动态信息和不确定性.具体而言,HVGNN使用双曲空间代替欧式空间,同时引入新的时间GNN(temporal GNN,TGNN)来建模动态特性.为了建模图的不确定性,HVGNN设计了一个基于TGNN的双曲VGAE,使模型可以对不确定性和动态进行联合建模.最后,引入的重参数化采样算法,实现模型的梯度学习.相较于欧式空间计算量的指数增长,双曲空间降低了模型的计算复杂度;对于不确定性的建模,增强了传递较少信息且具有较多动态特性节点的表示性能. ...
Hyperbolic neural networks
1
2018
... 动态图嵌入通常存在三方面的局限性:(1)嵌入表示空间[89 ,90 ] ,欧式空间表示可能导致图的潜在层次结构失真;(2)动态信息,忽视图的动态演化通常会导致模型错误地利用未来信息来预测过去的交互;(3)不确定性[91 ] ,图的固有特性,生成的确定性表示不能对不确定性建模.为了解决上述问题,HVGNN[92 ] 采用双曲变分GNN对双曲空间中的动态图进行建模,使生成的嵌入同时包含图的动态信息和不确定性.具体而言,HVGNN使用双曲空间代替欧式空间,同时引入新的时间GNN(temporal GNN,TGNN)来建模动态特性.为了建模图的不确定性,HVGNN设计了一个基于TGNN的双曲VGAE,使模型可以对不确定性和动态进行联合建模.最后,引入的重参数化采样算法,实现模型的梯度学习.相较于欧式空间计算量的指数增长,双曲空间降低了模型的计算复杂度;对于不确定性的建模,增强了传递较少信息且具有较多动态特性节点的表示性能. ...
Deep variational network embedding in Wasserstein space
1
2018
... 动态图嵌入通常存在三方面的局限性:(1)嵌入表示空间[89 ,90 ] ,欧式空间表示可能导致图的潜在层次结构失真;(2)动态信息,忽视图的动态演化通常会导致模型错误地利用未来信息来预测过去的交互;(3)不确定性[91 ] ,图的固有特性,生成的确定性表示不能对不确定性建模.为了解决上述问题,HVGNN[92 ] 采用双曲变分GNN对双曲空间中的动态图进行建模,使生成的嵌入同时包含图的动态信息和不确定性.具体而言,HVGNN使用双曲空间代替欧式空间,同时引入新的时间GNN(temporal GNN,TGNN)来建模动态特性.为了建模图的不确定性,HVGNN设计了一个基于TGNN的双曲VGAE,使模型可以对不确定性和动态进行联合建模.最后,引入的重参数化采样算法,实现模型的梯度学习.相较于欧式空间计算量的指数增长,双曲空间降低了模型的计算复杂度;对于不确定性的建模,增强了传递较少信息且具有较多动态特性节点的表示性能. ...
Hyperbolic variational graph neural network for modeling dynamic graphs
2
2021
... 动态图嵌入通常存在三方面的局限性:(1)嵌入表示空间[89 ,90 ] ,欧式空间表示可能导致图的潜在层次结构失真;(2)动态信息,忽视图的动态演化通常会导致模型错误地利用未来信息来预测过去的交互;(3)不确定性[91 ] ,图的固有特性,生成的确定性表示不能对不确定性建模.为了解决上述问题,HVGNN[92 ] 采用双曲变分GNN对双曲空间中的动态图进行建模,使生成的嵌入同时包含图的动态信息和不确定性.具体而言,HVGNN使用双曲空间代替欧式空间,同时引入新的时间GNN(temporal GNN,TGNN)来建模动态特性.为了建模图的不确定性,HVGNN设计了一个基于TGNN的双曲VGAE,使模型可以对不确定性和动态进行联合建模.最后,引入的重参数化采样算法,实现模型的梯度学习.相较于欧式空间计算量的指数增长,双曲空间降低了模型的计算复杂度;对于不确定性的建模,增强了传递较少信息且具有较多动态特性节点的表示性能. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Wavelets on graphs via spectral graph theory
1
2011
... 其中, A ˜ = A + I D ˜ A ˜ σ ( · ) H ( · ) H ( 0 ) X . 为了提高层间传播效率,GCN使用图上谱卷积一阶近似[93 ,94 ] .对于双层GCN模型,其前向传播公式为: ...
Convolutional neural networks on graphs with fast localized spectral filtering
1
2016
... 其中, A ˜ = A + I D ˜ A ˜ σ ( · ) H ( · ) H ( 0 ) X . 为了提高层间传播效率,GCN使用图上谱卷积一阶近似[93 ,94 ] .对于双层GCN模型,其前向传播公式为: ...
Graph attention networks
3
2017
... 图注意力网络(graph attention network,GAT)[95 ] 在GCN的基础上引入注意力机制[96 ] ,对邻近节点特征加权求和,分配不同的权值.针对单个节点,GAT使用self-attention[97 ] 获得注意力系数: ...
... DyRep[106 ] 将动态图嵌入假设为图的动态(拓扑演化)和图上的动态交织演化(节点间的活动)的中介过程.DyRep采用关联和通信事件的形式接收动态信息,并基于以下原则捕获观察到的事件的影响,更新有关节点的表示:(1)自我传播.自我传播是支配单个节点演化的动力中最小的组成部分.节点相对于其先前位置在嵌入空间中演化,而不是以随机方式进化.(2)外源驱动.一些外力可以在某时间间隔平滑地更新该节点的当前特征.(3)局部嵌入传播.事件中涉及的两个节点形成临时(通信)或永久(关联)路径,用于信息从一个节点的邻域传播到另一个节点.DyRep采用双时间尺度来捕捉图级和节点级的动态过程,计算节点表示并参数化.最后,使用时间注意机制[95 ,107 ] 耦合模型的结构和时间信息,使生成的节点嵌入可以捕获非线性的动态信息.DyRep作为一种归纳式学习模型,强调学习节点的表示方法而不是节点的固定表示,因此更利于新的节点表示的生成. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
An attentive survey of attention models
1
2019
... 图注意力网络(graph attention network,GAT)[95 ] 在GCN的基础上引入注意力机制[96 ] ,对邻近节点特征加权求和,分配不同的权值.针对单个节点,GAT使用self-attention[97 ] 获得注意力系数: ...
Attention is all you need
4
2017
... 图注意力网络(graph attention network,GAT)[95 ] 在GCN的基础上引入注意力机制[96 ] ,对邻近节点特征加权求和,分配不同的权值.针对单个节点,GAT使用self-attention[97 ] 获得注意力系数: ...
... 式中, e ij j i [97 ] 将注意力分配到节点i 的邻域: ...
... 式中, a [97 ] 生成节点嵌入: ...
... Transformer[97 ] 架构已经成为许多领域的主流选择,但在图级预测任务中,通常表现不佳.为此,Ying等人在标准Transformer的基础上利用图的结构信息构建Graphormer[119 ] (见图23 ).对于结构信息的编码主要分为三部分:(1)中心性编码(centrality encoding)用于捕捉图中节点的重要性,根据每个节点的度为每个节点分配一个可学习向量,并将其添加到输入层的节点特征中.(2)空间编码(spatial encoding)用于捕捉节点之间的结构关系,根据每个节点对的空间关系为其分配了一个可学习的嵌入.(3)边编码(edge encoding)用于捕捉边缘特征中额外的空间信息,然后将其输入到Transformer层.Graphormer同时使用上述结构信息编码,提升模型性能,进而生成更优的嵌入表示. ...
How powerful are graph neural networks?
2
2018
... 用于图嵌入的GNN模型大多遵循邻域聚合架构,通过递归地聚合和变换邻域节点的特征向量生成节点嵌入,因此不能有效区分某些简单的图结构.为了提高GNN模型对图结构的辨识能力,图同构网络(graph isomorphism network,GIN)[98 ] 利用GNN和WL(Weisfeiler-Lehman)图同构测试[99 ] 之间的密切联系,使生成的嵌入保留图结构辨识信息.WL测试通过聚合给定节点邻居的特征向量对该节点进行迭代更新,同时使用内射聚合更新将不同的节点邻域映射为不同的特征向量.GIN采用与WL内射聚合相似的方式进行建模:首先,将节点邻居的特征向量抽象为一个多集;然后,将邻居聚合运算抽象为多集上的函数(多集函数的区分性越强,底层的表征能力就越强);最后,将生成的嵌入用于图分类任务,其性能可以匹配WL测试的结果. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
A reduction of a graph to a canonical form and an algebra arising during this reduction
1
1968
... 用于图嵌入的GNN模型大多遵循邻域聚合架构,通过递归地聚合和变换邻域节点的特征向量生成节点嵌入,因此不能有效区分某些简单的图结构.为了提高GNN模型对图结构的辨识能力,图同构网络(graph isomorphism network,GIN)[98 ] 利用GNN和WL(Weisfeiler-Lehman)图同构测试[99 ] 之间的密切联系,使生成的嵌入保留图结构辨识信息.WL测试通过聚合给定节点邻居的特征向量对该节点进行迭代更新,同时使用内射聚合更新将不同的节点邻域映射为不同的特征向量.GIN采用与WL内射聚合相似的方式进行建模:首先,将节点邻居的特征向量抽象为一个多集;然后,将邻居聚合运算抽象为多集上的函数(多集函数的区分性越强,底层的表征能力就越强);最后,将生成的嵌入用于图分类任务,其性能可以匹配WL测试的结果. ...
Attribute2vec: deep network embedding through multi-filtering GCN
2
2020
... MF-GCN[100 ] 是一种多滤波GCN模型(见图19 ),在每个传播层使用多个局部GCN滤波器进行特征提取,使模型捕捉到节点特征的不同方面.对于第一层,MF-GCN对节点属性进行如下操作: ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Simplifying graph convolutional networks
1
2019
... 多数GCN模型中邻域相互作用项的系数相对较小,导致性能与采用线性策略的简化图卷积网络(simplified graph convolutional networks,SGC)[101 ] 相当.为了有效捕捉图的复杂非线性,GraphAIR[102 ] 同时对邻域聚合和邻域交互进行建模.GraphAIR由两部分组成:邻域聚合模块通过组合邻域特征来构建节点表示;邻域交互模块通过乘法运算显式建模邻域交互.现有的大多数GCN模型与GraphAIR兼容,可以提供即插即用的邻域聚合模块和邻域交互模块.此外,GraphAIR利用残差学习策略,将邻域交互与邻域聚合分离,使模型更容易优化. ...
Graphair: graph rep-resentation learning with neighborhood aggregation and interaction
2
2021
... 多数GCN模型中邻域相互作用项的系数相对较小,导致性能与采用线性策略的简化图卷积网络(simplified graph convolutional networks,SGC)[101 ] 相当.为了有效捕捉图的复杂非线性,GraphAIR[102 ] 同时对邻域聚合和邻域交互进行建模.GraphAIR由两部分组成:邻域聚合模块通过组合邻域特征来构建节点表示;邻域交互模块通过乘法运算显式建模邻域交互.现有的大多数GCN模型与GraphAIR兼容,可以提供即插即用的邻域聚合模块和邻域交互模块.此外,GraphAIR利用残差学习策略,将邻域交互与邻域聚合分离,使模型更容易优化. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
SDGNN: learning node representation for signed directed networks
2
2021
... SDGNN[103 ] 是用于处理符号有向图的嵌入模型,其在传统GNN的基础上考虑了平衡理论[104 ] 和地位理论[105 ] ,重新设计聚合器和损失函数.SDGNN聚合来自不同邻域的信息,并使用MLP(multilayer perceptron)将这些消息编码为节点嵌入.SDGNN的聚合器可分为两类:一是平均聚合器,二是注意力聚合器.为了优化生成的嵌入,SDGNN使用组合损失函数来重构网络中的符号、方向和三角形三个关键特征.平衡理论和地位理论的引入,使SDGNN在考虑边缘符号的同时兼顾方向信息,提升了模型在符号图分析任务中的表现. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Predicting positive and negative links in online social networks
1
2010
... SDGNN[103 ] 是用于处理符号有向图的嵌入模型,其在传统GNN的基础上考虑了平衡理论[104 ] 和地位理论[105 ] ,重新设计聚合器和损失函数.SDGNN聚合来自不同邻域的信息,并使用MLP(multilayer perceptron)将这些消息编码为节点嵌入.SDGNN的聚合器可分为两类:一是平均聚合器,二是注意力聚合器.为了优化生成的嵌入,SDGNN使用组合损失函数来重构网络中的符号、方向和三角形三个关键特征.平衡理论和地位理论的引入,使SDGNN在考虑边缘符号的同时兼顾方向信息,提升了模型在符号图分析任务中的表现. ...
Signed networks in social media
1
2010
... SDGNN[103 ] 是用于处理符号有向图的嵌入模型,其在传统GNN的基础上考虑了平衡理论[104 ] 和地位理论[105 ] ,重新设计聚合器和损失函数.SDGNN聚合来自不同邻域的信息,并使用MLP(multilayer perceptron)将这些消息编码为节点嵌入.SDGNN的聚合器可分为两类:一是平均聚合器,二是注意力聚合器.为了优化生成的嵌入,SDGNN使用组合损失函数来重构网络中的符号、方向和三角形三个关键特征.平衡理论和地位理论的引入,使SDGNN在考虑边缘符号的同时兼顾方向信息,提升了模型在符号图分析任务中的表现. ...
Dyrep: learning representations over dynamic graphs
2
2019
... DyRep[106 ] 将动态图嵌入假设为图的动态(拓扑演化)和图上的动态交织演化(节点间的活动)的中介过程.DyRep采用关联和通信事件的形式接收动态信息,并基于以下原则捕获观察到的事件的影响,更新有关节点的表示:(1)自我传播.自我传播是支配单个节点演化的动力中最小的组成部分.节点相对于其先前位置在嵌入空间中演化,而不是以随机方式进化.(2)外源驱动.一些外力可以在某时间间隔平滑地更新该节点的当前特征.(3)局部嵌入传播.事件中涉及的两个节点形成临时(通信)或永久(关联)路径,用于信息从一个节点的邻域传播到另一个节点.DyRep采用双时间尺度来捕捉图级和节点级的动态过程,计算节点表示并参数化.最后,使用时间注意机制[95 ,107 ] 耦合模型的结构和时间信息,使生成的节点嵌入可以捕获非线性的动态信息.DyRep作为一种归纳式学习模型,强调学习节点的表示方法而不是节点的固定表示,因此更利于新的节点表示的生成. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
GaAN: gated attention networks for learning on large and spatiotemporal graphs
1
2018
... DyRep[106 ] 将动态图嵌入假设为图的动态(拓扑演化)和图上的动态交织演化(节点间的活动)的中介过程.DyRep采用关联和通信事件的形式接收动态信息,并基于以下原则捕获观察到的事件的影响,更新有关节点的表示:(1)自我传播.自我传播是支配单个节点演化的动力中最小的组成部分.节点相对于其先前位置在嵌入空间中演化,而不是以随机方式进化.(2)外源驱动.一些外力可以在某时间间隔平滑地更新该节点的当前特征.(3)局部嵌入传播.事件中涉及的两个节点形成临时(通信)或永久(关联)路径,用于信息从一个节点的邻域传播到另一个节点.DyRep采用双时间尺度来捕捉图级和节点级的动态过程,计算节点表示并参数化.最后,使用时间注意机制[95 ,107 ] 耦合模型的结构和时间信息,使生成的节点嵌入可以捕获非线性的动态信息.DyRep作为一种归纳式学习模型,强调学习节点的表示方法而不是节点的固定表示,因此更利于新的节点表示的生成. ...
DySAT: deep neural representation learning on dynamic graphs via self-attention networks
2
2020
... DySAT[108 ] 通过邻域结构和时间两个维度的联合自注意力来计算节点嵌入,主体为三个模块(见图20 ):(1)结构注意力块通过自注意聚集和堆叠从每个节点局部邻域中提取特征,以计算每个快照的中间表示并输入到时间模块;(2)时间自注意力块通过嵌入每个快照的绝对时间位置[109 ] 来捕获排序信息,并将位置嵌入与结构注意力块的输出组合,输入到前馈层;(3)图上下文预测模块通过跨多个时间步长的目标函数保留节点的邻域信息,使生成的嵌入能够捕捉结构演化.DySAT的优点在于使用多头注意力 能够捕获动态性的多个方面,缺点在于该模型 仅适用于节点数恒定的动态图,并且节点共现率作为损失函数导致模型捕捉节点的动态变化的能力 有限. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Convol-utional sequence to sequence learning
1
2017
... DySAT[108 ] 通过邻域结构和时间两个维度的联合自注意力来计算节点嵌入,主体为三个模块(见图20 ):(1)结构注意力块通过自注意聚集和堆叠从每个节点局部邻域中提取特征,以计算每个快照的中间表示并输入到时间模块;(2)时间自注意力块通过嵌入每个快照的绝对时间位置[109 ] 来捕获排序信息,并将位置嵌入与结构注意力块的输出组合,输入到前馈层;(3)图上下文预测模块通过跨多个时间步长的目标函数保留节点的邻域信息,使生成的嵌入能够捕捉结构演化.DySAT的优点在于使用多头注意力 能够捕获动态性的多个方面,缺点在于该模型 仅适用于节点数恒定的动态图,并且节点共现率作为损失函数导致模型捕捉节点的动态变化的能力 有限. ...
EvolveGCN: evolving graph convolutional networks for dynamic graphs
2
2020
... 动态图中节点可能频繁出现和消失,使得RNN在学习这种不规则的行为时非常具有挑战性.为了解决这个问题,EvolveGCN[110 ] 在每个时间步使用RNN来调整GCN(即网络参数),即关注GCN参数在每个时刻的演化而不关注该时刻的节点表示,这不仅提高了模型的自适应性和灵活性,还可以保持图的动态信息.此外,EvolveGCN只对RNN参数进行训练,不再训练GCN参数,这种方式使得参数的数量不会随着时刻的增加而增长,使该模型像常用的RNN一样易于管理. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Streaming graph neural networks
2
2020
... 在新的边出现时,DGNN[111 ] 不仅更新节点表示,同时将交互信息传播到其他受影响的节点,使嵌入信息在更新和传播过程中可以合并交互之间的时间间隔.当新的边出现时,两端节点及其一阶邻域都有明显的概率变化.此外,邻域受到的影响与时刻有关,最近时刻与端点交互的邻居节点对出现的新变化很敏感,而较远的过去时刻的邻居受影响较小.端点和一阶邻域均使用时态信息增强LSTM作为更新模块的基本框架,使模型能够处理不同时间间隔的信息. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
TemporalGAT: attention-based dynamic graph representation learning
2
2020
... TemporalGAT[112 ] 通过集成GAT和时间卷积网络(temporal convolutional network,TCN)[113 ,114 ] 来学习动态图上的嵌入表示(见图21 ).该模型将self-attention应用于节点邻域,并通过TCN保留图的动态信息.最后,采用二元交叉熵损失函数[115 ] 学习节点表示,并预测节点之间是否存在边.TemporalGAT不仅能够建模节点数目不固定的动态图,还能同时捕获动态图的结构信息与时间信息. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
An empirical evalu-ation of generic convolutional and recurrent networks for sequence modeling
1
2018
... TemporalGAT[112 ] 通过集成GAT和时间卷积网络(temporal convolutional network,TCN)[113 ,114 ] 来学习动态图上的嵌入表示(见图21 ).该模型将self-attention应用于节点邻域,并通过TCN保留图的动态信息.最后,采用二元交叉熵损失函数[115 ] 学习节点表示,并预测节点之间是否存在边.TemporalGAT不仅能够建模节点数目不固定的动态图,还能同时捕获动态图的结构信息与时间信息. ...
Wavenet: a generative model for raw audio
1
2016
... TemporalGAT[112 ] 通过集成GAT和时间卷积网络(temporal convolutional network,TCN)[113 ,114 ] 来学习动态图上的嵌入表示(见图21 ).该模型将self-attention应用于节点邻域,并通过TCN保留图的动态信息.最后,采用二元交叉熵损失函数[115 ] 学习节点表示,并预测节点之间是否存在边.TemporalGAT不仅能够建模节点数目不固定的动态图,还能同时捕获动态图的结构信息与时间信息. ...
Dynamic graph repre-sentation learning via self-attention networks
1
2018
... TemporalGAT[112 ] 通过集成GAT和时间卷积网络(temporal convolutional network,TCN)[113 ,114 ] 来学习动态图上的嵌入表示(见图21 ).该模型将self-attention应用于节点邻域,并通过TCN保留图的动态信息.最后,采用二元交叉熵损失函数[115 ] 学习节点表示,并预测节点之间是否存在边.TemporalGAT不仅能够建模节点数目不固定的动态图,还能同时捕获动态图的结构信息与时间信息. ...
LINE: large-scale information network embedding
2
2015
... LINE[116 ] 同样定义了一阶相似度和二阶相似度函数,并对其进行优化.一阶相似度用于保持邻接矩阵和嵌入表示的点积接近,二阶相似度用于保持上下文节点的相似性.为了结合一阶和二阶相似度,LINE分别优化一阶和二阶相似度的目标函数,然后将生成的嵌入向量进行拼接.LINE的边采样策略克服了随机梯度下降的局限性,使其能够应用到大规模图嵌入中;但是一阶和二阶表示单独优化以及简单的拼接操作,限制了模型表示能力. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Deep recursive network embedding with regular equivalence
2
2018
... DRNE[117 ] 没有重建邻接矩阵,而是直接使用LSTM聚合邻域信息重建节点嵌入(见图22 ).DRNE的目标函数如下:由于LSTM要求其输入是一个序列,DRNE根据节点的度数进行排序,同时对度数较大的节点采用邻域抽样技术,以防止过长的记忆.这种方法可以保持节点的正则等价性和多种中心性度量(如PageRank[118 ] ). ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
The PageRank citation ranking: bringing order to the Web[R]
1
1999
... DRNE[117 ] 没有重建邻接矩阵,而是直接使用LSTM聚合邻域信息重建节点嵌入(见图22 ).DRNE的目标函数如下:由于LSTM要求其输入是一个序列,DRNE根据节点的度数进行排序,同时对度数较大的节点采用邻域抽样技术,以防止过长的记忆.这种方法可以保持节点的正则等价性和多种中心性度量(如PageRank[118 ] ). ...
Do transformers really perform bad for graph representation?
2
2021
... Transformer[97 ] 架构已经成为许多领域的主流选择,但在图级预测任务中,通常表现不佳.为此,Ying等人在标准Transformer的基础上利用图的结构信息构建Graphormer[119 ] (见图23 ).对于结构信息的编码主要分为三部分:(1)中心性编码(centrality encoding)用于捕捉图中节点的重要性,根据每个节点的度为每个节点分配一个可学习向量,并将其添加到输入层的节点特征中.(2)空间编码(spatial encoding)用于捕捉节点之间的结构关系,根据每个节点对的空间关系为其分配了一个可学习的嵌入.(3)边编码(edge encoding)用于捕捉边缘特征中额外的空间信息,然后将其输入到Transformer层.Graphormer同时使用上述结构信息编码,提升模型性能,进而生成更优的嵌入表示. ...
... Strategies of static graph embedding
Table 2 模型分类 模型 时间 模型策略 矩阵分解 LLE[24 ] 2000 构造邻域保持映射,最小化重建损失函数 GF[13 ] 2013 分解邻接矩阵,利用向量内积捕捉边的存在 GraRep[25 ] 2015 使用SVD分解k 步对数转移概率矩阵 HOPE[27 ] 2016 GSVD分解相似度矩阵,L2范数保持高阶相似度 NGE[30 ] 2013 使用NMF将输入分解为系数矩阵和嵌入矩阵 LE[32 ] 2001 保持相连节点在嵌入空间尽可能靠近 CGE[33 ] 2011 修改LE损失函数,保持低权值节点对相似性 SPE[34 ] 2009 利用核矩阵生成关系矩阵 A ˜ A A ˜ 随机游走 Deepwalk[49 ] 2014 使用随机游走采样节点,Skip-Gram最大化节点共现概率 node2vec[50 ] 2016 在Deepwalk的基础上引入有偏的随机游走 HARP[51 ] 2017 利用原始图生成保留全局结构的压缩图 Walklets[52 ] 2016 改进Deepwalk,捕获节点与社区的从属关系并建模 TriDNR[54 ] 2016 最大化节点标签、节点邻域、节点内容的共现概率 自编码器 GraphEncoder[63 ] 2014 利用L2损失函数重构图相似度矩阵 SDNE[64 ] 2016 使用有监督和无监督组件分别保持一阶和二阶相似度 DNGR[65 ] 2016 随机冲浪捕获图结构,生成PPMI矩阵输入SDAE DNE-APP[67 ] 2017 使用PPMI度量和k 步转移矩阵构建相似度聚合矩阵 VGAE[69 ] 2016 引入VAE,使用GCN编码器,使用内积解码器 GALA[73 ] 2020 编码器执行拉普拉斯平滑,解码器执行拉普拉斯锐化 ANE[76 ] 2018 施加对抗性正则化避免流形断裂 图神经网络 GCN[70 ] 2016 利用谱卷积一阶近似提高层间传播效率 GraphSAGE[85 ] 2017 采样和聚合节点的局部邻域特征训练聚合器函数 GAT[95 ] 2017 在GCN的基础上引入self-attention和multi-head attention GIN[98 ] 2018 利用GNN和WL图同构测试保留图结构信息 MF-GCN[100 ] 2020 使用多个局部GCN滤波器提取节点特征 GraphAIR[102 ] 2020 邻域聚合模块融合节点特征表示,邻域交互模块通过乘法运算显示建模 SDGNN[103 ] 2021 在GNN的基础引入地位理论和平衡理论 其他 LINE[116 ] 2015 分别优化一阶和二阶相似度,将嵌入向量进行拼接 DNRE[117 ] 2018 直接使用LSTM聚合邻域信息重建节点嵌入 Graphormer[119 ] 2021 在标准Transformer基础上,引入有中心性编码、空间编码和边编码
表3 动态图嵌入模型策略归纳 ...
Embedding temporal network via neighborhood formation
2
2018
... HTNE[120 ] 使用Hawkes过程[121 ] 捕捉历史邻域对当前邻域的影响,建模动态图中节点的邻域序列.然后,将节点分别映射为基向量和历史向量,并输入到Hawkes过程以生成嵌入表示.由于历史邻域对当前邻域形成的影响因节点而不同,引入注意力机制调节影响的大小.HTNE的核心在于使用邻域的形成过程描述节点的动态演化,Hawkes过程及注意力的引入使生成的嵌入有效集成到上述信息. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Spectral of some self-exciting and mutually exciting point processes
1
1971
... HTNE[120 ] 使用Hawkes过程[121 ] 捕捉历史邻域对当前邻域的影响,建模动态图中节点的邻域序列.然后,将节点分别映射为基向量和历史向量,并输入到Hawkes过程以生成嵌入表示.由于历史邻域对当前邻域形成的影响因节点而不同,引入注意力机制调节影响的大小.HTNE的核心在于使用邻域的形成过程描述节点的动态演化,Hawkes过程及注意力的引入使生成的嵌入有效集成到上述信息. ...
Dynamic network embedding by modeling triadic closure process
2
2018
... DynamicTriad[122 ] 通过施加三元组(一组三个顶点的集合)模拟图的动态变化.一般来说,三元组分为两种类型:闭合三元组和开放三元组.由开放三元组演化为封闭三元组的三元组闭合过程是动态图形成和演化的基本机制[123 ,124 ] .DynamicTriad采用统一的框架来量化上述闭合过程,使模型能够有效捕捉图的动态信息. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
1
1994
... DynamicTriad[122 ] 通过施加三元组(一组三个顶点的集合)模拟图的动态变化.一般来说,三元组分为两种类型:闭合三元组和开放三元组.由开放三元组演化为封闭三元组的三元组闭合过程是动态图形成和演化的基本机制[123 ,124 ] .DynamicTriad采用统一的框架来量化上述闭合过程,使模型能够有效捕捉图的动态信息. ...
Triadic closure pattern analysis and prediction in social networks
1
2015
... DynamicTriad[122 ] 通过施加三元组(一组三个顶点的集合)模拟图的动态变化.一般来说,三元组分为两种类型:闭合三元组和开放三元组.由开放三元组演化为封闭三元组的三元组闭合过程是动态图形成和演化的基本机制[123 ,124 ] .DynamicTriad采用统一的框架来量化上述闭合过程,使模型能够有效捕捉图的动态信息. ...
Temporal network embe-dding with micro-and macro-dynamics
2
2019
... 动态图通常是在微观和宏观两方面随时间演化,微观动态可以描述拓扑结构的形成过程,宏观动态描述了图规模的演化模式.M2 DNE[125 ] 是首个将微观动态和宏观动态同时融入到动态图嵌入过程的模型.对于微观动态,M2 DNE把边的建立当作时间事件,并提出时间注意点流程来捕获用于嵌入生成的时间属性.对于宏观动态,M2 DNE通过定义使用嵌入参数化的动态方程来捕获内在演化模式,再利用内在演化模式在更高层次上约束图的拓扑结构.最后,M2 DNE利用微观动态和宏观动态的演化和交互,生成节点嵌入.微观动态描述的是网络结构的形成过程,宏观动态描述的是网络规模的演化模式.大多数动态图方法只考虑了微观动态,忽略了宏观动态在保持网络结构和演化模式方面的重要价值,M2 DNE同时使用宏观动态和微观动态,进而增强了模型的泛化能力. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Inductive repres-entation learning in temporal networks via causal anon-ymous walks
2
2021
... 因果匿名游走(causal anonymous walks,CAW)[126 ] 与匿名游走(anonymous walks,AW)[127 ] 相比有两个不同性质:(1)因果关系提取.CAW从感兴趣的链接开始,随着时间的推移回溯多个相邻链接,以编码动态图的基本因果关系.(2)基于集合的匿名化.CAW删除遍历集合中的节点标识以保证归纳学习,同时根据特定位置出现的计数对相应节点标识进行编码.CAW-N是专门用于链接预测的变体,该模型对两个感兴趣的节点进行CAW采样,然后通过RNN和集合池化对采样结果进行编码和聚合,生成最终嵌入.CAW-N不仅保留了游走过程中所有细粒度的时间信息,还可以通过motif [128 ,129 ] 计数将其移除. ...
... Strategies of dynamic graph embedding
Table 3 模型分类 模型 时间 模型策略 矩阵分解 DANE[36 ] 2017 拉普拉斯特征映射捕获t 时刻的结构和属性信息,矩阵摄动理论更新动态信息 DHPE[38 ] 2018 GSVD分解各时刻Katz矩阵,矩阵摄动理论更新动态信息 TRIP[40 ] 2015 利用图中三角形个数构建特征函数,将特征对矩阵映射成嵌入向量 TIMERS[41 ] 2017 SVD最大误差界重启,消除增量更新积累的误差 DWSF[45 ] 2017 将图中有限监督信息合并为标签,并在每次迭代中更新 随机游走 CTDNE[56 ] 2018 按照时间顺序对边进行遍历 dynnode2vec[57 ] 2018 node2vec初始化快照,对变化点执行随机游走,利用Skip-Gram更新动态信息 STWalk[59 ] 2017 捕捉规定时间窗内节点的变化 tNodeEmbed[60 ] 2019 模仿句子嵌入作为节点嵌入,捕捉节点角色和边的动态变化 自编码器 DynGEM[78 ] 2018 提出PropSize动态调节神经元个数,同时引入L1和L2正则化 dyngraph2vec[79 ] 2019 组合AE和LSTM,构建不同的编码器和解码器组合 NetWalk[81 ] 2018 同时最小化节点距离和自编码器重构误差 BurstGraph[84 ] 2019 将动态演化分为一般演化和突发演化,RNN捕捉各时刻的图结构 HVGNN[92 ] 2021 采用基于TGNN的双曲VGAE 图神经网络 DyRep[106 ] 2018 基于自我传播、外源驱动、局部嵌入传播更新节点表示 DySAT[108 ] 2020 结构注意力提取邻域特征,时间注意力捕捉多个时刻的表示 EvolveGCN[110 ] 2019 在每个时刻使用RNN调整GCN参数 DGNN[111 ] 2020 使用时态信息增强LSTM作为更新框架 TemporalGAT[112 ] 2020 集成GAT和TCN,self-attention应用于邻域,TCN用于动态信息更新 其他 HTNE[120 ] 2018 Hawkes捕捉过去时刻对当前时刻邻域的影响,Skip-Gram更新动态信息 DynamicTriad[122 ] 2018 通过闭合三元组和开放三元组模拟图的动态演化 M2 DNE[125 ] 2019 微观动态描述结构的形成,宏观动态描述规模的演化,利用二者交互生成嵌入 CAW[126 ] 2021 回溯多个时刻的相邻链接编码因果关系,根据特征位置计数编码相应节点标识
图嵌入模型之间不是相互割裂的,而是存在理论依托关系:CGE修改LE的目标函数,进一步增强邻近节点相似性;DANE离线模型采用类似LE的方式保持各时刻快照的一阶相似度;DHPE以HOPE为基础,引入矩阵摄动理论更新动态信息;NGE、MF和DWSF以NMF为基础;node2vec在Deepwalk的基础上引入有偏的随机游走;HARP通常与Deepwalk或node2vec结合使用;dynnode2vec在node2vec的基础上,使用Skip-Gram更新动态信息;DNE-APP在DNGR基础上引入成对约束;VGAE使用GCN作为编码器;BurstGraph使用GraphSAGE进行采样;GAT在GCN的基础上引入注意力机制;MF-GCN以GraphSAGE为基础构建;GraphAIR将GCN和GAT作为组件;EvolveGCN使用RNN调整GCN参数;TemporalGAT对GAT和TCN进行集成. ...
Reconstructing Markov processes from independent and anonymous experiments
1
2016
... 因果匿名游走(causal anonymous walks,CAW)[126 ] 与匿名游走(anonymous walks,AW)[127 ] 相比有两个不同性质:(1)因果关系提取.CAW从感兴趣的链接开始,随着时间的推移回溯多个相邻链接,以编码动态图的基本因果关系.(2)基于集合的匿名化.CAW删除遍历集合中的节点标识以保证归纳学习,同时根据特定位置出现的计数对相应节点标识进行编码.CAW-N是专门用于链接预测的变体,该模型对两个感兴趣的节点进行CAW采样,然后通过RNN和集合池化对采样结果进行编码和聚合,生成最终嵌入.CAW-N不仅保留了游走过程中所有细粒度的时间信息,还可以通过motif [128 ,129 ] 计数将其移除. ...
Efficient graphlet counting for large networks
1
2015
... 因果匿名游走(causal anonymous walks,CAW)[126 ] 与匿名游走(anonymous walks,AW)[127 ] 相比有两个不同性质:(1)因果关系提取.CAW从感兴趣的链接开始,随着时间的推移回溯多个相邻链接,以编码动态图的基本因果关系.(2)基于集合的匿名化.CAW删除遍历集合中的节点标识以保证归纳学习,同时根据特定位置出现的计数对相应节点标识进行编码.CAW-N是专门用于链接预测的变体,该模型对两个感兴趣的节点进行CAW采样,然后通过RNN和集合池化对采样结果进行编码和聚合,生成最终嵌入.CAW-N不仅保留了游走过程中所有细粒度的时间信息,还可以通过motif [128 ,129 ] 计数将其移除. ...
Motifs in temporal networks
1
2017
... 因果匿名游走(causal anonymous walks,CAW)[126 ] 与匿名游走(anonymous walks,AW)[127 ] 相比有两个不同性质:(1)因果关系提取.CAW从感兴趣的链接开始,随着时间的推移回溯多个相邻链接,以编码动态图的基本因果关系.(2)基于集合的匿名化.CAW删除遍历集合中的节点标识以保证归纳学习,同时根据特定位置出现的计数对相应节点标识进行编码.CAW-N是专门用于链接预测的变体,该模型对两个感兴趣的节点进行CAW采样,然后通过RNN和集合池化对采样结果进行编码和聚合,生成最终嵌入.CAW-N不仅保留了游走过程中所有细粒度的时间信息,还可以通过motif [128 ,129 ] 计数将其移除. ...
Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks
1
1990
... 图嵌入可以解释为生成图数据的向量表示,用于洞察图的某种特性.表2 和表3 归纳了主要静态图嵌入和动态图嵌入的模型策略.基于矩阵分解的方法只有包含特定的目标函数,才能学习相应的图结构和信息.基于随机游走的方法可以通过改变参数来控制游走方式,还可以与其他模型叠加提升性能.基于AE和GNN的方法利用近似定理[130 ] 广泛建模,使模型能够同时学习节点属性、拓扑结构和节点标签等信息. ...
Social computing data repository
1
2009
... Flickr[131 ] :由照片分享网站Flickr上的用户组成的网络.网络中的边指示用户之间的联系关系.标签指示用户的兴趣组(例如黑白色摄影). ...
Scalable learning of collective behavior based on sparse social dimensions
1
2009
... YouTube[132 ] :YouTube视频分享网站用户之间的社交网络.标签代表了喜欢视频类型(例如动漫视频)的观众群体. ...
Network repres-entation learning with rich text information
1
2015
... Wikipedia[133 ] :网页共现网络,节点表示网页,边表示网页之间的超链接.Wikipedia数据集的TF-IDF矩阵是描述节点特征的文本信息,节点标签是网页的类别. ...
Collective classi-fication in network data
1
2008
... Cora、CiteSeer、Pubmed[134 ] :标准的引文网络基准数据集,节点表示论文,边表示一篇论文对另一篇论文的引用.节点特征是论文的词袋表示,节点标签是论文的学术主题. ...
Graphsaint: graph sampling based inductive learning method
1
2019
... Yelp[135 ] :本地商业评论和社交网站,用户可以提交对商家的评论,并与其他人交流.由于缺乏标签信息,该数据集常用于链接预测. ...
mTrust: discerning multi-faceted trust in a connected world
1
2012
... Epinions[136 ] :产品评论网站数据集,基于评论的词袋模型生成节点属性,以用户评论的主要类别作为类别标签.该数据集有16个时间戳. ...
Overview of the 2003 KDD Cup
1
2003
... Hep-th[137 ] :高能物理理论会议研究人员的合作网络,原始数据集包含1993年1月至2003年4月期间高能物理理论会议的论文摘要. ...
1
2021
... AS(autonomous systems)[138 ] :由边界网关协议日志构建的用户通信网络.该数据集包含从1997年11月8日到2000年1月2日的733条通信记录,通常按照年份将这些记录划分为不同快照. ...
The enron corpus: a new dataset for email classification research
1
2004
... Enron[139 ] :Enron公司员工之间的电子邮件通信网络.该数据集包含1999年1月至2002年7月期间公司员工之间的电子邮件. ...
Patterns and dynamics of users’ behavior and interaction: network analysis of an online community
1
2009
... UCI[140 ] :加州大学在线学生社区用户之间的通信网络.节点表示用户,用户之间的消息通信表示边缘.每条边携带的时间指示用户何时通信. ...
Adapting information retri-eval systems to user queries
1
2008
... 网络重构任务通常采用MAP(mean average pre-cision)[141 ] 作为评价指标: ...
Applied logistic regression
1
2000
... 节点分类任务通常分为3个步骤:(1)使用图嵌入模型生成嵌入表示.(2)将包含标签信息的数据集划分为训练集和测试集.(3)在训练集上训练分类器,在测试集验证模型性能.常用的分类器包括逻辑回归分类器[142 ] 、最近邻分类器[143 ] 、支持向量机[144 ] 和朴素贝叶斯分类器[145 ] 等. ...
Scikit-learn: machine learning in Python
1
2011
... 节点分类任务通常分为3个步骤:(1)使用图嵌入模型生成嵌入表示.(2)将包含标签信息的数据集划分为训练集和测试集.(3)在训练集上训练分类器,在测试集验证模型性能.常用的分类器包括逻辑回归分类器[142 ] 、最近邻分类器[143 ] 、支持向量机[144 ] 和朴素贝叶斯分类器[145 ] 等. ...
Least squares support vector machine classifiers
1
1999
... 节点分类任务通常分为3个步骤:(1)使用图嵌入模型生成嵌入表示.(2)将包含标签信息的数据集划分为训练集和测试集.(3)在训练集上训练分类器,在测试集验证模型性能.常用的分类器包括逻辑回归分类器[142 ] 、最近邻分类器[143 ] 、支持向量机[144 ] 和朴素贝叶斯分类器[145 ] 等. ...
A comparison of event models for Naive Bayes text classification
1
1998
... 节点分类任务通常分为3个步骤:(1)使用图嵌入模型生成嵌入表示.(2)将包含标签信息的数据集划分为训练集和测试集.(3)在训练集上训练分类器,在测试集验证模型性能.常用的分类器包括逻辑回归分类器[142 ] 、最近邻分类器[143 ] 、支持向量机[144 ] 和朴素贝叶斯分类器[145 ] 等. ...
A tutorial on spectral clustering
1
2007
... 聚类任务采用无监督的方式将图划分为若干个社区,使属于同一社区的节点具有更多相似特性.在利用模型生成嵌入后,一般采用频谱聚类(非归一化谱聚类[146 ] 和归一化谱聚类[147 ] )和k -means[148 ] 等经典方法将节点嵌入聚类. ...
Normalized cuts and image seg-mentation
1
2000
... 聚类任务采用无监督的方式将图划分为若干个社区,使属于同一社区的节点具有更多相似特性.在利用模型生成嵌入后,一般采用频谱聚类(非归一化谱聚类[146 ] 和归一化谱聚类[147 ] )和k -means[148 ] 等经典方法将节点嵌入聚类. ...
Some methods for classification and analysis of multivariate observations
1
1966
... 聚类任务采用无监督的方式将图划分为若干个社区,使属于同一社区的节点具有更多相似特性.在利用模型生成嵌入后,一般采用频谱聚类(非归一化谱聚类[146 ] 和归一化谱聚类[147 ] )和k -means[148 ] 等经典方法将节点嵌入聚类. ...
Graph regularized nonnegative matrix factorization for data representation
1
2011
... 聚类任务通常采用归一化互信息(normalized mutual information,NMI)[149 ] 评估聚类性能: ...
Fast memory-efficient anomaly detection in streaming heterogeneous graphs
1
2016
... 异常检测任务用于识别图中的“非正常”结构,通常包括异常节点检测、异常边缘检测和异常变化检测.常见的异常检测方法有两种:一是将原始图进行压缩,通过聚类和离群点检测识别压缩图中的异常[150 ,151 ] ;二是利用模型生成节点嵌入并分组为k 个社群,检测不属于已有社群的新节点或边. ...
A scalable approach for outlier detection in edge streams using sketch-based approximations
1
2016
... 异常检测任务用于识别图中的“非正常”结构,通常包括异常节点检测、异常边缘检测和异常变化检测.常见的异常检测方法有两种:一是将原始图进行压缩,通过聚类和离群点检测识别压缩图中的异常[150 ,151 ] ;二是利用模型生成节点嵌入并分组为k 个社群,检测不属于已有社群的新节点或边. ...
Visualizing large-scale and high-dimensional data
1
2016
... 对于可视化任务,好的嵌入表示在二维图像中相同或相近的节点彼此接近,不同的节点彼此分离.在Cora数据集上,将模型生成的低维嵌入输入到t -SNE[10 ,152 ] ,使嵌入维数降至2,同一类别的节点使用相同的颜色表示.Yuan等人[153 ] 比较了不同模型的可视化性能,部分可视化结果见图28 .GCN和GAT学习的节点向量能够有效捕捉到社区的结构,使同类型节点更为接近.Deepwalk和SDNE只使用邻接矩阵作为输入,没有充分利用节点特征和标签信息,导致模型性能较差,尤其是SDNE模型,不同类型的点在二维空间中几乎是无序的. ...
Semi- AttentionAE: an integrated model for graph representation learning
2
2021
... 对于可视化任务,好的嵌入表示在二维图像中相同或相近的节点彼此接近,不同的节点彼此分离.在Cora数据集上,将模型生成的低维嵌入输入到t -SNE[10 ,152 ] ,使嵌入维数降至2,同一类别的节点使用相同的颜色表示.Yuan等人[153 ] 比较了不同模型的可视化性能,部分可视化结果见图28 .GCN和GAT学习的节点向量能够有效捕捉到社区的结构,使同类型节点更为接近.Deepwalk和SDNE只使用邻接矩阵作为输入,没有充分利用节点特征和标签信息,导致模型性能较差,尤其是SDNE模型,不同类型的点在二维空间中几乎是无序的. ...
... 大部分图嵌入模型生成的结果将用于节点分类、链接预测、可视化等多个任务.与上述建模思路不同,面向任务的嵌入模型只关注一个任务,并充分利用与该任务相关信息来训练模型.多数情况下,面向任务的嵌入模型在目标任务上比通用嵌入模型更有效,如Semi-AttentionAE[153 ] 采用集成学习的方法,联合训练GAT与LE,提升节点分类任务性能.针对特定任务设计高性能模型同样是今后研究的热点方向. ...
Open graph benchmark: datasets for machine learning on graphs
1
2020
... 对于大规模静态图嵌入,通常采用分布式计算或无监督学习的方式提高计算效率.开放图基准(open graph benchmark,OGB)[154 ] 是新兴图学习领域可扩展、可重复的基准,通过验证node2vec、LINE和GraphSAGE等实验表现,证明了模型的有效性.对于大规模动态图嵌入,现有模型无法采用类似静态图的方式实现图表示学习任务,因为动态图的规模不仅涉及图的大小,还涉及快照或时间戳的数量.因此,降低网络演化复杂度和提升模型性能是解决大规模动态图嵌入问题的两个重要方面. ...
Heterogeneous graph structure learning for graph neural networks
1
2021
... 现阶段,大部分研究仍集中在简单的同质图上,如经典的GCN模型只需邻接矩阵、节点特征矩阵和系数矩阵即可实现.然而,现实世界的网络往往更加复杂,如异质图、有向图和超图等.现有模型中,HGSL[155 ] 实现了异质图表示学习,SDGNN实现了符号有向图表示学习,DANE实现了属性图的表示学习.随着图表示学习研究的深入,探索更为复杂图数据的表示将仍旧是有前景的研究方向. ...
The art of data augmentation
1
2001
... 复杂的模型可以提升效果,但往往超参数较多且难以训练.相较于设计新的模型架构,一些研究者开始探索如何利用训练策略(如数据扩增[156 ] )来提升现有模型的性能.GraphMix[157 ] 利用数据扩增技术,将简单的GCN架构提升到先进基线模型的水平,并且无需额外的内存和计算消耗.现阶段,除了开发新的图嵌入模型外,充分挖掘已有模型潜力仍然是一项充满挑战的工作. ...
GraphMix: improved training of GNNs for semi-supervised learning
1
2019
... 复杂的模型可以提升效果,但往往超参数较多且难以训练.相较于设计新的模型架构,一些研究者开始探索如何利用训练策略(如数据扩增[156 ] )来提升现有模型的性能.GraphMix[157 ] 利用数据扩增技术,将简单的GCN架构提升到先进基线模型的水平,并且无需额外的内存和计算消耗.现阶段,除了开发新的图嵌入模型外,充分挖掘已有模型潜力仍然是一项充满挑战的工作. ...